题目内容
 如图,已知正比例函数y=ax与反比例函数y=
如图,已知正比例函数y=ax与反比例函数y=| k |
| x |
(1)求a、k的值;
(2)若双曲线y=
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把A点坐标分别代入y=ax与y=
可计算出a=
,k=8;
(2)作CM⊥x轴于M,AN⊥x轴于N,设C点坐标为(t,
),由于S△AOC=S△OCM+S梯形ANMC-S△OAN,根据反比例函数k的几何意义得到4+
(2+
)•|4-t|-4=15,整理得到t2+15t-16=0或t2-15t-16=0,然后解两个一元二次方程,再确定满足条件的t的值,最后写出C点坐标.
| k |
| x |
| 1 |
| 2 |
(2)作CM⊥x轴于M,AN⊥x轴于N,设C点坐标为(t,
| 8 |
| t |
| 1 |
| 2 |
| 8 |
| t |
解答:解: (1)把A(4,2)分别代入y=ax与y=
(1)把A(4,2)分别代入y=ax与y=
得4a=2,2=
,
所以a=
,k=8;
(2)作CM⊥x轴于M,AN⊥x轴于N,如图,
反比例函数解析式为y=
,
设C点坐标为(t,
)(t>0),
∵△AOC的面积为15,
∴S△AOC=S△OCM+S梯形ANMC-S△OAN,
∴4+
(2+
)•|4-t|-4=15,
整理得t2+15t-16=0,解得t=1,t=-16(舍去),
或t2-15t-16=0,解得t=-1(舍去),t=16,
∴C点坐标为(1,8)、(16,
).
 (1)把A(4,2)分别代入y=ax与y=
(1)把A(4,2)分别代入y=ax与y=| k |
| x |
| k |
| 4 |
所以a=
| 1 |
| 2 |
(2)作CM⊥x轴于M,AN⊥x轴于N,如图,
反比例函数解析式为y=
| 8 |
| x |
设C点坐标为(t,
| 8 |
| t |
∵△AOC的面积为15,
∴S△AOC=S△OCM+S梯形ANMC-S△OAN,
∴4+
| 1 |
| 2 |
| 8 |
| t |
整理得t2+15t-16=0,解得t=1,t=-16(舍去),
或t2-15t-16=0,解得t=-1(舍去),t=16,
∴C点坐标为(1,8)、(16,
| 1 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.

练习册系列答案
相关题目
把二次函数y=x2-2x+4化成顶点式为( )
| A、y=(x-1)2+2 |
| B、y=(x+1)2+3 |
| C、y=(x-1)2 |
| D、y=(x-1)2+3 |
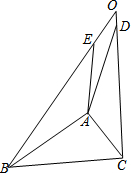 如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O.
如图,AB、AD是以AB为边向△ABC向外所作正n边形的一组邻边;AC、AE是以AC为边向△ABC外所作正n边形的一组邻边,BE、CD的延长线相交于点O.