题目内容
20. 小红看到这样一道题“如图,AC=AD,BA平分∠CBD,求证:BC=BD”她很快给出了证明过程如下:
小红看到这样一道题“如图,AC=AD,BA平分∠CBD,求证:BC=BD”她很快给出了证明过程如下:证明:∵BA平分∠CBD∴∠ABC=∠ABD
在△ABC和△ABD中,AC=AD,∠ABD=∠ABD,AB=AB
∴△ABC≌△ABD∴BC=BD
你认为她的证明过程正确吗?正确说出每一步的理论证据;不正确,请你写出正确的证明过程.
分析 过A作AE⊥BC交BC延长线于E,AF⊥BD交BD延长线于F,则∠E=∠F=90°,根据角平分线性质得出AE=AF,∠EBA=∠FBA,根据HL求出Rt△AEC≌Rt△AFD,根据全等得出EC=FD,同理BE=BF,即可得出答案.
解答 不正确,
证明:
过A作AE⊥BC交BC延长线于E,AF⊥BD交BD延长线于F,
则∠E=∠F=90°,
∵BA平分∠CBD,AE⊥BC交BC,AF⊥BD,
∴AE=AF,∠EBA=∠FBA,
在Rt△AEC和Rt△AFD中
$\left\{\begin{array}{l}{AC=AD}\\{AE=AF}\end{array}\right.$
∴Rt△AEC≌Rt△AFD(HL),
∴EC=FD,
同理Rt△AEB≌Rt△AFB,
∴BE=BF,
∴BE-EC=BF-FD,
∴BC=BD.
点评 本题考查了全等三角形的性质和判定,角平分线性质的应用,解此题的关键是能求出Rt△AEC≌Rt△AFD和Rt△AEB≌Rt△AFB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.已知代数式3x2-6x+6的值为9,则代数式x2-2x+8的值为( )
| A. | 18 | B. | 9 | C. | 12 | D. | 7 |
 如图,某城市A地和B地之间经常有车辆来往,C地和D地之间也经常有车辆来往,建立如图所示的直角坐标系,四个地方的坐标分别为A(-3,2)、B(-1,-4)、C(-5,-3)、D(1,1),要拟建一个加油站,那么加油站建在哪里,对大家都方便?给出具体位置.
如图,某城市A地和B地之间经常有车辆来往,C地和D地之间也经常有车辆来往,建立如图所示的直角坐标系,四个地方的坐标分别为A(-3,2)、B(-1,-4)、C(-5,-3)、D(1,1),要拟建一个加油站,那么加油站建在哪里,对大家都方便?给出具体位置.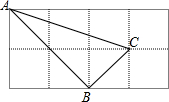 如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点上,这样的三角形叫做格点三角形,请画出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形可以画几个?
如图,在2×4的方格纸中,△ABC的3个顶点都在小正方形的顶点上,这样的三角形叫做格点三角形,请画出另一个格点三角形DEF,使△DEF≌△ABC,这样的三角形可以画几个? 已知如图,抛物线y=ax2+bx+2与x轴相交于B(x1,0)、C(x2,0)(x1,x2均大于0)两点,与y轴的正半轴相交于A点.过A、B、C三点的⊙P与y轴相切于点A,其面积为$\frac{25π}{4}$.
已知如图,抛物线y=ax2+bx+2与x轴相交于B(x1,0)、C(x2,0)(x1,x2均大于0)两点,与y轴的正半轴相交于A点.过A、B、C三点的⊙P与y轴相切于点A,其面积为$\frac{25π}{4}$. 如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么BE的长是8 cm.
如图,△ABC≌△BAD,AC与BD是对应边,AC=8cm,AD=10cm,DE=CE=2cm,那么BE的长是8 cm.