��Ŀ����
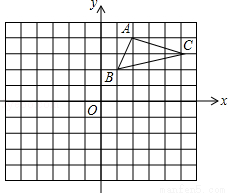
������12�֣���ͼ����ƽ��ֱ�������У���OΪ����ԭ�㣬ֱ��y=��x+4��x�ύ�ڵ�A������A��������y=ax2+bx��ֱ��y=��x+4������һ��B���ҵ�B�ĺ�����Ϊ1��

��1����a��b��ֵ����3�֣�
��2����P���߶�AB��һ���㣨��P�����A��B�غϣ�������P��PM��OB����һ�����ڵ��������ڵ�M������M��MC��x���ڵ�C����AB�ڵ�N������P��PF��MC�ڵ�F����PF�ij�Ϊt��MN�ij�Ϊd����d��t֮��ĺ�����ϵʽ����Ҫ��д���Ա���t��ȡֵ��Χ������4�֣�
��3����ͼ��3������ֱ��AB�Ƶ�A˳ʱ����ת15�Ƚ������߶Գ����ڵ�C, ��PΪ�߶�OA�ϵ�һ�����㣨���O����A���غϣ����Ե�OΪԲ�ġ���OPΪ�뾶��Բ�����߶�OC���ڵ�M���Ե�AΪԲ�ġ���APΪ�뾶��Բ�����߶�AC���ڵ�N������MN���ڵ�P�˶��Ĺ����У��ı���OMNA����������ֵ��������Сֵ���������ֵ����5�֣�
��1��a=��1��b=4����2��d=4t����3���ı���OMNB���������Сֵ����СֵΪ3 ��
��
��������
�����������1��������֪�ó�A��B�����꣬�������ô���ϵ������a��b��ֵ��
��2����֪MN=d��PF=t����ͼ��֪MN=MF+FN��������MF��FN��PF���棬���ɵõ�MN��PF�Ĺ�ϵ������45���ֱ�������κ�ƽ�������ʿ��Ƶ�FN=PF=t����MPF=��BOD��������tan��BOD=tan��MPF���� =
= =3���Ӷ���MF=3PF=3t���Ӷ��ó�d��t�ĺ�����ϵ��
=3���Ӷ���MF=3PF=3t���Ӷ��ó�d��t�ĺ�����ϵ��
��3����OP=m���ı���OMNB�����ΪS��������ON��AM����֤��OAN�ա�ACM��SAS������֪CM��AN��AP��AB=BC=4����M��MF��AC,����ΪF,��MF=MCsin60= ���ֱ��ʾ��OAC�͡�MNC�������Ȼ��������IJ�õ��ı���OMNB�����ΪS�����ݹ�ϵʽ����ֵ��
���ֱ��ʾ��OAC�͡�MNC�������Ȼ��������IJ�õ��ı���OMNB�����ΪS�����ݹ�ϵʽ����ֵ��
�����������������
��1����y=��x+4��x�ύ�ڵ�A����A��4��0����
�ߵ�B�ĺ�����Ϊ1����ֱ��y=��x+4������B����B��1��3����
��������y=ax2+bx����A��4��0����B��1��3����
�� ����ã�
����ã� ����a=��1��b=4��
����a=��1��b=4��
��2����ͼ����BD��x���ڵ�D���ӳ�MP��x���ڵ�E��
��B��1��3����A��4��0������OD=1��BD=3��OA=4��
��AD=3����AD=BD��
�ߡ�BDA=90�㣬��BAD=��ABD=45�㣬
��MC��x�ᣬ���ANC=��BAD=45�㣬
���PNF=��ANC=45�㣬��PF��MC�����FPN=��PNF=45�㣬
��NF=PF=t��
�ߡ�DFM=��ECM=90�㣬��PF��EC��
���MPF=��MEC����ME��OB�����MEC=��BOD��
���MPF=��BOD����tan��BOD=tan��MPF���� =
= =3��
=3��
��MF=3PF=3t����MN=MF+FN����d=3t+t=4t��

��3���ı���OMNB���������Сֵ��
��OP=m���ı���OMNB�����ΪS��������ON��AM��
��֤��OAN�ա�ACM��SAS������֪CM��AN��AP��
AB=BC=4�� S��ABC= ��42=
��42= ����CM=AN= AP=4��m��CN=OP=m��
����CM=AN= AP=4��m��CN=OP=m��
��M��MF��AC,����ΪF,
��MF=MCsin60= ��
��
��S��CMN= =
=
 =
= ��
��
��S=S��OAC��S��CMN
= ����
���� ��
��
= ��
��
���ڵ�P�˶��Ĺ����У��ı���OMNA���������СֵΪ3 ��
��

���㣺���κ����ۺ��⣻���������ε��ж������ʣ����ɶ�����
��������� ����1�����κ��� ���壺һ��أ����
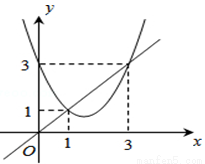
 ��a��b��c�dz�����a��0������ôy����x �Ķ��κ�����
��a��b��c�dz�����a��0������ôy����x �Ķ��κ����� ����ν���κ�������˵�Ա�����ߴ�����2;
�ڶ��κ���
 ��a��0����x��y�DZ�����a��b��c�dz������Ա���x ��ȡֵ��Χ��ȫ��ʵ����b��c����������ʵ����a�Dz�����0��ʵ������Ϊa=0ʱ��
��a��0����x��y�DZ�����a��b��c�dz������Ա���x ��ȡֵ��Χ��ȫ��ʵ����b��c����������ʵ����a�Dz�����0��ʵ������Ϊa=0ʱ�� ��Ϊy=bx+c��b��0,��y=bx+c��һ�κ�������b=0����y=c��һ������������
��Ϊy=bx+c��b��0,��y=bx+c��һ�κ�������b=0����y=c��һ�������������۶��κ���
 ��a��0����һԪ���η���
��a��0����һԪ���η��� ��a��0����������ϵ�����������y����һ����������ô������κ�������һ��һԪ���κ�����
���κ����Ľ���ʽ��������ʽ��
��a��0����������ϵ�����������y����һ����������ô������κ�������һ��һԪ���κ�����
���κ����Ľ���ʽ��������ʽ�� ��1��һ��ʽ��
 ��a��b��c�dz�����a��0����
��a��b��c�dz�����a��0���� ��2������ʽ��
 ��a��h��k�dz�����a��0��
��a��h��k�dz�����a��0�� ��3����������
 ��x���н���ʱ������Ӧ���κ÷���
��x���н���ʱ������Ӧ���κ÷��� ��ʵ��x1��x2����ʱ�����ݶ�������ʽ�ķֽ���ʽ
��ʵ��x1��x2����ʱ�����ݶ�������ʽ�ķֽ���ʽ �����κ���
�����κ��� ��ת��Ϊ����ʽ
��ת��Ϊ����ʽ �����û�н��㣬����������ʾ��
�����û�н��㣬����������ʾ�� ���κ�����һ����ʽ�Ľṹ������
�ٺ����Ĺ�ϵʽ����ʽ��
���Ա�������ߴ�����2��
�۶�����ϵ���������㡣 ���κ������ж���
���κ�����һ����ʽ�еȺ��ұ��ǹ����Ա���x�Ķ�������ʽ��
��b=0��c=0ʱ��y=ax2������Ķ��κ�����
�ж�һ�������Dz��Ƕ��κ������ڹ�ϵʽ����ʽ��ǰ���£�����ѹ�ϵʽ����������ȥ���š��ϲ�ͬ�������д��
 ��a��0������ʽ����ô����������Ƕ��κ���������Ͳ��ǡ�
��������
��a��0������ʽ����ô����������Ƕ��κ���������Ͳ��ǡ�
��������
- ���ͣ�
- �Ѷȣ�
- ���ˣ�
- �꼶��

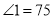 ����
���� �Ĵ�С�ǣ� ����
�Ĵ�С�ǣ� ����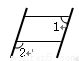
 = ��
= ��