Question

如果一个正整数能表示为两个连续偶数的平方差，那么称这个正整数为“神秘数”．如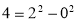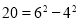， ，，因此4，12，20都是“神秘数”

（1）28和2012这两个数是“神秘数”吗？为什么？

（2）设两个连续偶数为2k+2和2k（其中k取非负整数），由这两个连续偶数构造的神秘数是4的倍数吗？为什么？

（3）两个连续奇数的平方差（取正数）是神秘数吗？为什么？

Answer 1

（1）是，理由见解析；（2）是，理由见解析；（3）不是，理由见解析．

【解析】

试题分析：（1）根据“神秘数”的定义，只需看能否把28和2012这两个数写成两个连续偶数的平方差即可判断；

（2）运用平方差公式进行计算，进而判断即可；

（3）运用平方差公式进行计算，进而判断即可．

试题解析：1、28=4×7=8-6

2012=4×503=504-502

∴这两个数都是神秘数

2、 （2k+2）-（2k）

=（2k+2-2k）（2k+2+2k）

=2×[2（k+1+k）]

=4（2k+1）

∴由2k+2和2k构造的神秘数是4的倍数

3、设两个连续奇数为2k+1和2k-1，

则（2k+1）-（2k-1）

=（2k+1+2k-1）（2k+1-2k+1）

=4k×2

=8k，

∴两个连续奇数的平方差不是神秘数

考点：完全平方公式；平方差公式．

考点分析： 考点1：整式 （1）概念：单项式和多项式统称为整式．
他们都有次数，但是多项式没有系数，多项式的每一项是一个单项式，含有字母的项都有系数．
（2）规律方法总结：
①对整式概念的认识，凡分母中含有字母的代数式都不属于整式，在整式范围内用“+”或“-”将单项式连起来的就是多项式，不含“+”或“-”的整式绝对不是多项式，而单项式注重一个“积”字．
②对于“数”或“形”的排列规律问题，用先从开始的几个简单特例入手，对比、分析其中保持不变的部分及发展变化的部分，以及变化的规律，尤其变化时与序数几的关系，归纳出一般性的结论． 试题属性

• 题型：
• 难度：
• 考核：
• 年级：