题目内容
观察表格:

根据表格解答下列问题:(1)a=_______,b=_______,c=_______.
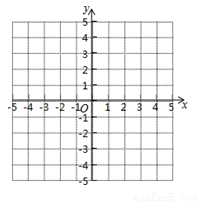
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c<-3成立;
(1)1,-2,-3;(2)0<x<2.
【解析】
试题分析:(1)直接将(1,1)代入求出a即可,进而将x=2代入求出y,再分别将(0,-3),(2,-3)代入求出b,c的值;
(2)再利用函数解析式进而得出函数图象,进而得出不等式的解集.
试题解析:(1)∵y=ax2过(1,1),
∴1=a,
∴当x=2时,y=22=4,
∵y=ax2+bx+c过(0,-3),(2,-3),a=1,
∴c=-3,-3=22+2b-3,
解得:b=-2,
∴y=x2-2x-3,

(2)0<x<2.
考点:1.二次函数与不等式(组);2.二次函数的图象.

练习册系列答案
相关题目
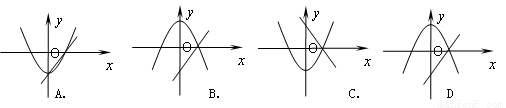
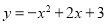 .
.
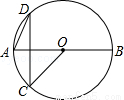
 x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止.
x2+bx+c的图象经过B、C两点.现将一把直尺放置在直角坐标系中,使直尺的边A'D'∥y轴且经过点B,直尺沿x轴正方向平移,当A'D'与y轴重合时运动停止. 时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.
时,线段PA、PB、PC之间的数量关系.请直接写出结论,并指出相应的点P与抛物线的位置关系.

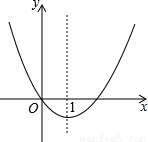

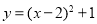 ,则当 x≥2时,y随x增大的变化规律是( )
,则当 x≥2时,y随x增大的变化规律是( )