题目内容
11.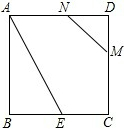 如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.
如图,正方形ABCD的边长为2,BE=CE,MN=1,线段MN的两端点在CD、AD上滑动,当DM为( )时,△ABE与以D、M、N为顶点的三角形相似.| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{2\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{5}}}{5}$或$\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$或$\frac{{3\sqrt{5}}}{5}$ |
分析 根据AE=EB,△ABE中,AB=2BE,所以在△MNC中,分CM与AB和BE是对应边两种情况利用相似三角形对应边成比例求出CM与CN的关系,然后利用勾股定理列式计算即可.
解答 解:∵四边形ABCD是正方形,
∴AB=BC,
∵BE=CE,
∴AB=2BE,
又∵△ABE与以D、M、N为顶点的三角形相似,
∴①DM与AB是对应边时,DM=2DN
∴DM2+DN2=MN2=1
∴DM2+$\frac{1}{4}$DM2=1,
解得DM=$\frac{2\sqrt{5}}{5}$;
②DM与BE是对应边时,DM=$\frac{1}{2}$DN,
∴DM2+DN2=MN2=1,
即DM2+4DM2=1,
解得DM=$\frac{\sqrt{5}}{5}$.
∴DM为$\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$时,△ABE与以D、M、N为顶点的三角形相似.
故选C.
点评 本题考查相似三角形的判定与性质、正方形的性质.解决本题特别要考虑到①DM与AB是对应边时,②当DM与BE是对应边时这两种情况.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
16.下列生活中的现象,属于平移的是( )
| A. | 升降电梯从底楼升到顶楼 | B. | 闹钟的钟摆的运动 | ||
| C. | DVD片在光驱中运行 | D. | 秋天的树叶从树上随风飘落 |





 如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?
如图,小明把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,他发现2∠A=∠1+∠2,你能帮他解释其中的原因吗?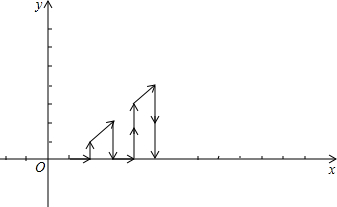 如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).
如图,在平面直角坐标系中,有若干个横坐标和纵坐标都是整数的点,其顺序排列规律如下:(1,0),(2,0),(2,1),(3,2),(3,1),(3,0),…,根据这个规律探究可得,第100个点的坐标为(14,8);第2015个点的坐标(63,3).