题目内容
14.计算或化简:(1)2cos30°-$\frac{3}{\sqrt{3}}$+($\frac{1}{3}$)0+(-1)2017
(2)(1+$\frac{1}{m}$)÷$\frac{{m}^{2}-1}{{m}^{2}-2m+1}$.
分析 (1)原式利用特殊角的三角函数值,二次根式性质,零指数幂法则,以及乘方的意义计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=2×$\frac{\sqrt{3}}{2}$-$\sqrt{3}$+1-1=0;
(2)原式=$\frac{m+1}{m}$•$\frac{(m-1)^{2}}{(m+1)(m-1)}$=$\frac{1}{m}$.
点评 此题考查了分式的混合运算,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
2.下列运算正确的是( )
| A. | a2•a3=a6 | B. | (a3)2=a9 | C. | a4+b4=(a+b)4 | D. | (a6)2÷(a4)3=1 |
4.把$\frac{{-\sqrt{45{y^2}}}}{{3\sqrt{5y}}}$化简后得( )
| A. | $\frac{{-\sqrt{9y}}}{3}$ | B. | $-\sqrt{y}$ | C. | $-3\sqrt{5y}$ | D. | $\frac{{3\sqrt{5}}}{5}$ |
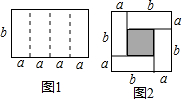 如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).
如图1是一个长为4a、宽为b的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2). 如图,已知点C为AB上一点,AC=15cm,CB=$\frac{3}{5}$AC,D,E分别为AC,AB的中点,求DE的长.
如图,已知点C为AB上一点,AC=15cm,CB=$\frac{3}{5}$AC,D,E分别为AC,AB的中点,求DE的长.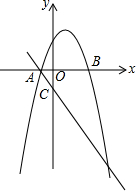 在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.
在平面直角坐标系xOy中,抛物线y=-x2+bx+c与x轴交于点A,B(A在B的左侧),抛物线的对称轴为直线x=1,AB=4.