题目内容
15.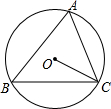 如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.
如图,⊙O为△ABC的外接圆,∠A=72°,则∠BCO的度数为18°.
分析 连结OB,如图,先根据圆周角定理得到∠BOC=2∠A=144°,然后根据等腰三角形的性质和三角形内角和定理计算∠BCO的度数.
解答  解:连结OB,如图,∠BOC=2∠A=2×72°=144°,
解:连结OB,如图,∠BOC=2∠A=2×72°=144°,
∵OB=OC,
∴∠CBO=∠BCO,
∴∠BCO=$\frac{1}{2}$(180°-∠BOC)=$\frac{1}{2}$×(180°-144°)=18°.
故答案为:18°.
点评 本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰三角形的性质.

练习册系列答案
相关题目
5.如果|a+1|=3,则a的值为( )
| A. | 1 | B. | 3 | C. | 2或-4 | D. | 2或-3 |
5.若x>y,则下列不等式中不成立的是( )
| A. | x-a>y-a | B. | 3-x>3-y | C. | x+2>y+2 | D. | $\frac{x}{3}>\frac{y}{3}$ |
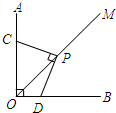 已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD.
已知:∠AOB=∠CPD=90°,OM是∠AOB的平分线,求证:PC=PD. 如图,已知CD为△ABC的高,∠ACB=90°,AC=6cm,BC=8cm,AB=10cm,则CD=$\frac{24}{5}$cm.
如图,已知CD为△ABC的高,∠ACB=90°,AC=6cm,BC=8cm,AB=10cm,则CD=$\frac{24}{5}$cm.