题目内容
已知:o为坐标原点,∠ AOB=300 , ∠ABO=900 且A(2,0)求: 过A、B、O三点的二次函数解析式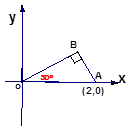

解析考点:待定系数法求二次函数解析式.
分析:过B点作BC⊥OA,垂足为C,解Rt△OAB可求OB,解Rt△OBC可求OC、BC,确定B点坐标,根据O、A、B三点坐标,设交点式求二次函数解析式.
解答:
解:过B点作BC⊥OA,垂足为C,
在Rt△OAB中,OA=2,∠AOB=30°,
∴OB= ,
,
在Rt△OBC中,OB= ,∠BOC=30°,
,∠BOC=30°,
∴OC= ,BC=
,BC= ,
,
即B( ,
, ),
),
∵抛物线过O(0,0),A(2,0),
设抛物线解析式为y=ax(x-2),将B( ,
, )代入,得
)代入,得 (
( -2)a=
-2)a= ,
,
解得a=- ,
,
∴二次函数解析式为y=- x(x-2)=-
x(x-2)=- x
x +
+ x.
x.
点评:本题考查了用待定系数法求二次函数解析式的方法.关键是根据条件确定抛物线解析式的形式,再求其中的待定系数.一般式:y=ax +bx+c(a≠0);顶点式y=a(x-h)
+bx+c(a≠0);顶点式y=a(x-h) +k,其中顶点坐标为(h,k);交点式y=a(x-x
+k,其中顶点坐标为(h,k);交点式y=a(x-x )(x-x
)(x-x ),抛物线与x轴两交点为(x
),抛物线与x轴两交点为(x ,0),(x
,0),(x ,0).
,0).

练习册系列答案
相关题目
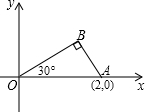 已知:O为坐标原点,∠AOB=30°,∠ABO=90°且A(2,0).求:过A、B、O三点的二次函数解析式.
已知:O为坐标原点,∠AOB=30°,∠ABO=90°且A(2,0).求:过A、B、O三点的二次函数解析式.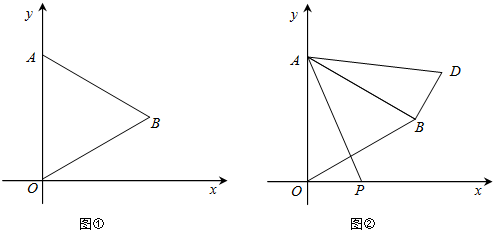
 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0). 如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).
如图,已知点O为坐标原点,∠AOB=30°,∠B=90°,且点A的坐标为(2,0).