题目内容
（2012•和平区一模）在平面直角坐标系中，已知点O为坐标原点，点A（0，4）．△AOB是等边三角形，点B在第一象限．
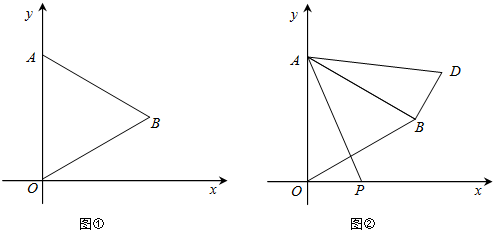
（Ⅰ）如图①，求点B的坐标；
（Ⅱ）点P是x轴上的一个动点，连接AP，以点A为旋转中心，把△AOP逆时针旋转，使边AO与AB重合，得△ABD．
①如图②，当点P运动到点（
，0）时，求此时点D的坐标；
②求在点P运动过程中，使△OPD的面积等于
的点P的坐标（直接写出结果即可）．
（Ⅰ）如图①，求点B的坐标；
（Ⅱ）点P是x轴上的一个动点，连接AP，以点A为旋转中心，把△AOP逆时针旋转，使边AO与AB重合，得△ABD．
①如图②，当点P运动到点（
| 3 |
②求在点P运动过程中，使△OPD的面积等于
| ||
| 4 |
分析：（I）过点B作BE⊥y轴于点E，作BF⊥x轴于点F．依题意得BF=OE=2，利用勾股定理求出OF，然后可得点B的坐标．
（II）①由△ABD由△AOP旋转得到，证明△ABD≌△AOP．AP=AD，∠DAB=∠PAO，∠DAP=∠BAO=60°，△ADP是等边三角形．利用勾股定理求出DP．在Rt△BDG中，∠BGD=90°，∠DBG=60°．利用三角函数求出BG=BD•cos60°，DG=BD•sin60°．然后求出OH，DH，然后求出点D的坐标．
②本题分三种情况进行讨论，设点P的坐标为（x，0）：第一种情况：当点P在x轴正半轴上时，第二种情况：当P在x轴负半轴，OP＜
时，第三种情况：当点P在x轴的负半轴上，且OP≥
时，此时点D在x轴上或第四象限．综合上面三种情况即可求出符合条件的值．
（II）①由△ABD由△AOP旋转得到，证明△ABD≌△AOP．AP=AD，∠DAB=∠PAO，∠DAP=∠BAO=60°，△ADP是等边三角形．利用勾股定理求出DP．在Rt△BDG中，∠BGD=90°，∠DBG=60°．利用三角函数求出BG=BD•cos60°，DG=BD•sin60°．然后求出OH，DH，然后求出点D的坐标．
②本题分三种情况进行讨论，设点P的坐标为（x，0）：第一种情况：当点P在x轴正半轴上时，第二种情况：当P在x轴负半轴，OP＜
4
| ||
| 3 |
4
| ||
| 3 |
解答：
解：（Ⅰ）如图①，过点B作BE⊥y轴于点E，作BF⊥x轴于点F，
∵△AOB是等边三角形，OA=4，
∴BF=OE=2．
在Rt△OBF中，
由勾股定理，得OF=
=2
．
∴点B的坐标为（2
，2）．
（Ⅱ）①如图②，过点B作BE⊥y轴于点E，作BF⊥x轴于点F，过点D作DH⊥x轴于点H，
延长EB交DH于点G．
则BG⊥DH．
∵△ABD由△AOP旋转得到，
∴△ABD≌△AOP．
∴∠ABD=∠AOP=90°，BD=OP=
．
∵△AOB是等边三角形，
∴∠ABO=60°．
∵BE⊥OA，
∴∠ABE=30°，∴∠DBG=60°，∠BDG=30°．
在Rt△DBG中，BG=
DB=
OP=
．
∵sin60°=
，∴DG=DB•sin60°=
×
=
．
∴OH=2
+
=
．DH=2+
=
．
∴点D的坐标为（
，
）．
②点P的坐标分别为（
，0）、（-
，0）、（-
，0）、
（
，0）．
假设存在点P，在它运动过程中，使△OPD的面积等于
．
设OP=x，下面分三种情况讨论．
第一种情况：
当点P在x轴正半轴上时，如图③，BD=OP=x，
在Rt△DBG中，∠DBG=60°，
∴DG=BD•sin60°=
x．
∴DH=2+
x．
∵△OPD的面积等于
，
∴
x•(2+
x)=
，
x2+4x-
=0．
解得：x1=
，x2=
（舍去）．
∴点P1的坐标为（
，0）．
第二种情况：
当点P在x轴的负半轴上，且OP＜
时，此时点D在第一象限，如图④，
在Rt△DBG中，∠DBG=30°，BG=BD•cos30°=
x．
∴DH=GH=2-
x．
∵△OPD的面积等于
，
∴
x•(2-
x)=
，
x2-4x+
=0．
解得：x1=
，x2=
．
∴点P2的坐标为（-
，0）．点P3的坐标为（-
，0）．
第三种情况：
当点P在x轴的负半轴上，且OP≥
时，此时点D在x轴上或第四象限，如图⑤，
在Rt△DBG中，∠DBG=60°，
∴DG=BD•sin60°=
x．
∵△OPD的面积等于
，
∴
x•(
x-2)=
，
x2-4x-
=0．
解得：x1=
，x2=
（舍去）．
∴点P4的坐标为（
，0）．
综上所述，点P的坐标为：P1（
，0）、P2（-
，0）、P3（-
，0）、P4（
，0）．
解：（Ⅰ）如图①，过点B作BE⊥y轴于点E，作BF⊥x轴于点F，∵△AOB是等边三角形，OA=4，
∴BF=OE=2．
在Rt△OBF中，
由勾股定理，得OF=
| OB2-BF2 |
| 3 |
∴点B的坐标为（2
| 3 |
（Ⅱ）①如图②，过点B作BE⊥y轴于点E，作BF⊥x轴于点F，过点D作DH⊥x轴于点H，
延长EB交DH于点G．
则BG⊥DH．
∵△ABD由△AOP旋转得到，
∴△ABD≌△AOP．
∴∠ABD=∠AOP=90°，BD=OP=
| 3 |
∵△AOB是等边三角形，
∴∠ABO=60°．
∵BE⊥OA，
∴∠ABE=30°，∴∠DBG=60°，∠BDG=30°．
在Rt△DBG中，BG=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
∵sin60°=
| DG |
| DB |
| 3 |
| ||
| 2 |
| 3 |
| 2 |
∴OH=2
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
| 3 |
| 2 |
| 7 |
| 2 |
∴点D的坐标为（
| 5 |
| 2 |
| 3 |
| 7 |
| 2 |
②点P的坐标分别为（
| ||||
| 3 |
| ||
| 3 |
| 3 |
（
-
| ||||
| 3 |
假设存在点P，在它运动过程中，使△OPD的面积等于
| ||
| 4 |
设OP=x，下面分三种情况讨论．
第一种情况：
当点P在x轴正半轴上时，如图③，BD=OP=x，
在Rt△DBG中，∠DBG=60°，
∴DG=BD•sin60°=
| ||
| 2 |
∴DH=2+
| ||
| 2 |
∵△OPD的面积等于
| ||
| 4 |
∴
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 3 |
解得：x1=
-2
| ||||
| 3 |
-2
| ||||
| 3 |
∴点P1的坐标为（
| ||||
| 3 |
第二种情况：
当点P在x轴的负半轴上，且OP＜
4
| ||
| 3 |
在Rt△DBG中，∠DBG=30°，BG=BD•cos30°=
| ||
| 2 |
∴DH=GH=2-
| ||
| 2 |
∵△OPD的面积等于
| ||
| 4 |
∴
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 3 |
解得：x1=
| ||
| 3 |
| 3 |
∴点P2的坐标为（-
| ||
| 3 |
| 3 |
第三种情况：
当点P在x轴的负半轴上，且OP≥
4
| ||
| 3 |
在Rt△DBG中，∠DBG=60°，
∴DG=BD•sin60°=
| ||
| 2 |
∵△OPD的面积等于
| ||
| 4 |
∴
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
| 3 |
| 3 |
解得：x1=
2
| ||||
| 3 |
2
| ||||
| 3 |
∴点P4的坐标为（
-
| ||||
| 3 |
综上所述，点P的坐标为：P1（
| ||||
| 3 |
| ||
| 3 |
| 3 |
-
| ||||
| 3 |
点评：本题主要考查了旋转的性质、等边三角形的性质和二次函数的性质，关于动点问题，注意分类讨论解答．
练习册系列答案
相关题目
