��Ŀ����
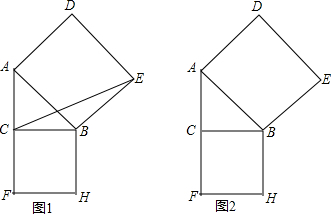
9���ڡ�ABC�У���ACB=90�㣬�ֱ���AB��BCΪ��������������ADEB��������BCFH����1����BC=mʱ��������BCFH���ܳ�= ���ú�m�Ĵ���ʽ��ʾ����
��2������CE����˵����������BEC���������������BCFH�����һ�룮
��3����֪AC=BC=2���ҵ�P���߶�DE�ϵĶ��㣬��Q���߶�BC�ϵĶ��㣬��P���Q�����ƶ������У���APQ���ܳ��Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
���� ��1��ֱ���������ε����ʵó��𰸼��ɣ�
��2������AH��֤����BHA�ա�BCE�����á�BHA�����=��BCE������ó����ۣ�
��3������A����DE�ĶԳƵ�A�䣬��A����BC�ĶԳƵ�F�����öԳƵ����ʵó���APQ���ܳ�����СֵΪA��F����һ��������⼴�ɣ�
��� �⣺��1�����ı���BCFH�������Σ�
��BC=BH=FH=CF��
�൱BC=mʱ��������BCFH���ܳ�Ϊ4m��
�ʴ�Ϊ��4m��
��2����ͼ1������AH��
�ڡ�BHA�͡�BCE�У�
$\left\{\begin{array}{l}{AB=BE}\\{��CBE=��ABH}\\{BC=BH}\end{array}\right.$
���BHA�ա�BCE��SAS����
���BHA�����=��BCE�����=$\frac{1}{2}$������BCFH�������
��3����APQ���ܳ�������Сֵ��
��ͼ2������A����DE�ĶԳƵ�A
��AP=A��P
�ߵ�A����BC�ĶԳƵ�F��
��AQ=QF��
���APQ���ܳ�����СֵΪA��F��
��A����A��M��FA��FA���ӳ�����M��
�ߡ�AA��MΪ����ֱ�������Σ�
��AA��=4$\sqrt{2}$��
��MA=MA��=4��
��MF=8��A��F=4$\sqrt{5}$��
���APQ���ܳ�����СֵΪ4$\sqrt{5}$��
���� �����ۺϿ��������ε����ʣ��ԳƵ����ʣ����ɶ����������Լ����öԳ�������̾�������⣬��������̾�������������˽�ģ˼������ã�ע�⸨���ߵ�������

 ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д� ���ɶ���ܲ��¿�ֱͨ��Уϵ�д�
���ɶ���ܲ��¿�ֱͨ��Уϵ�д�| A�� | a=3��b=2 | B�� | a��3��b=-2 | C�� | a=-3��b��-2 | D�� | a=3��b=-2 |
 �����ҹ������������������������Ⱦ���أ�ij����Ϊ�̻��������ƻ�����ס����������繲��n�ã��йؼס��������������Ϣ��ͼ��ʾ��
�����ҹ������������������������Ⱦ���أ�ij����Ϊ�̻��������ƻ�����ס����������繲��n�ã��йؼס��������������Ϣ��ͼ��ʾ��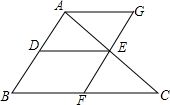 ��ͼ��DE�ǡ�ABC����λ�ߣ�����E��AB��ƽ���߽�BC�ڵ�F������A��BC��ƽ���߽�ֱ��EF�ڵ�G���߶�DE��BF��FC֮���������Ĺ�ϵ����֤����Ľ��ۣ�
��ͼ��DE�ǡ�ABC����λ�ߣ�����E��AB��ƽ���߽�BC�ڵ�F������A��BC��ƽ���߽�ֱ��EF�ڵ�G���߶�DE��BF��FC֮���������Ĺ�ϵ����֤����Ľ��ۣ� ij��ѧ�IJ���ѧ���μӸ�����ѧ��֪ʶ������С��ͬѧͳ�������в���ͬѧ�ijɼ������Ҹ���ѧ����֪ʶ������ͳ��ͼ����ͼ���������ͼ���ṩ����Ϣ�ش����⣺
ij��ѧ�IJ���ѧ���μӸ�����ѧ��֪ʶ������С��ͬѧͳ�������в���ͬѧ�ijɼ������Ҹ���ѧ����֪ʶ������ͳ��ͼ����ͼ���������ͼ���ṩ����Ϣ�ش����⣺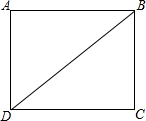 ����ABCD�У�AB=4��AD=3��P��Q�ǶԽ���BD�ϲ��غϵ����㣬��P����ֱ��AD��AB�ĶԳƵ�ֱ���E��F����Q����ֱ��BC��CD�ĶԳƵ�ֱ��ǵ�G��H�����ɵ�E��F��G��H���ɵ��ı���ǡ��Ϊ���Σ���PQ�ij���
����ABCD�У�AB=4��AD=3��P��Q�ǶԽ���BD�ϲ��غϵ����㣬��P����ֱ��AD��AB�ĶԳƵ�ֱ���E��F����Q����ֱ��BC��CD�ĶԳƵ�ֱ��ǵ�G��H�����ɵ�E��F��G��H���ɵ��ı���ǡ��Ϊ���Σ���PQ�ij���