题目内容
14. 如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2,回答下列问题:
如图,抛物线y1=-x2+2向右平移1个单位得到的抛物线y2,回答下列问题:(1)抛物线y2的顶点坐标是什么?
(2)阴影部分的面积S=2.
(3)若再将抛物线y2沿x轴翻折得到抛物线y3,求抛物线y3的解析式.
分析 (1)先确定二次函数y=-x2+2的顶点坐标为(0,2),然后根据点平移的规律得到点(0,2)平移后所得对应点的坐标为(1,2);
(2)阴影部分的面积可转化为平行四边形的面积,然后根据平行四边形的面积公式求解;
(3)根据关于x轴对称的点的坐标特征得到点(1,2)关于x轴对称的点的坐标为(1,-2),由于抛物线沿x轴翻折时开口方向改变,所以可利用顶点式得到抛物线y3的解析式.
解答 解:(1)抛物线y1=-x2+2向右平移1个单位得到的抛物线y2=-(x-1)2+2,
则抛物线y2的顶点坐标为(1,2);
(2)阴影部分的面积S=1×2=2;
故答案为2;
(3)抛物线y2=-(x-1)2+2的顶点坐标为(1,2),
而点(1,2)关于x轴对称的点的坐标为(1,-2),
所以抛物线y3的解析式为y=(x-1)2-2.
点评 本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.也考查了关于x轴对称的点的坐标特征.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.瓷器商店委托搬运站送800只瓷花瓶,双方约定每只运费是3角5分,若打破1只,这只不但不给运费,反而要赔偿2元5角钱,结果运到目的地后,搬运站共得运费268.6元,问在搬运过程中打破了多少只瓷花瓶?
6. 安徽省蒙城县板桥中学办学特色好,“校园文化”建设,主体鲜明新颖:“国学引领,教老敬亲,家校一体,爱满乡村”.如图所示,若用“C4”表示“孝”,则“A5-B4-C3-C5”表示( )
安徽省蒙城县板桥中学办学特色好,“校园文化”建设,主体鲜明新颖:“国学引领,教老敬亲,家校一体,爱满乡村”.如图所示,若用“C4”表示“孝”,则“A5-B4-C3-C5”表示( )
 安徽省蒙城县板桥中学办学特色好,“校园文化”建设,主体鲜明新颖:“国学引领,教老敬亲,家校一体,爱满乡村”.如图所示,若用“C4”表示“孝”,则“A5-B4-C3-C5”表示( )
安徽省蒙城县板桥中学办学特色好,“校园文化”建设,主体鲜明新颖:“国学引领,教老敬亲,家校一体,爱满乡村”.如图所示,若用“C4”表示“孝”,则“A5-B4-C3-C5”表示( )| A. | 爱满乡村 | B. | 教老敬亲 | C. | 国学引领 | D. | 板桥中学 |
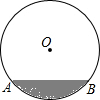 在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.
在半径为17dm的圆柱形油罐内装进一些油后,横截面如图.