题目内容
(本题满分12分)问题提出:平面内不在同一条直线上的三点确定一个圆.那么平面内的四点(任意三点均不在同一直线上),能否在同一个圆呢?
初步思考:设不在同一条直线上的三点 、
、 、
、 确定的圆为⊙
确定的圆为⊙ .
.
(1)当 、
、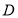 在线段
在线段 的同侧时,
的同侧时,

如图①,若点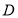 在⊙
在⊙ 上,此时有
上,此时有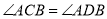 ,理由是 ;
,理由是 ;
如图②,若点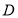 在⊙
在⊙ 内,此时有
内,此时有
 ;
;
如图③,若点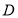 在⊙
在⊙ 外,此时有
外,此时有
 .(填“
.(填“ ”、“
”、“ ”或“
”或“ ”);
”);
由上面的探究,请直接写出 、
、 、
、 、
、 四点在同一个圆上的条件: .
四点在同一个圆上的条件: .
类比学习:(2)仿照上面的探究思路,请探究:当 、
、 在线段
在线段 的异侧时的情形.
的异侧时的情形.

如图④,此时有 ,如图⑤,此时有 ,
如图⑥,此时有 .
由上面的探究,请用文字语言直接写出 、
、 、
、 、
、 四点在同一个圆上的条件:
四点在同一个圆上的条件:
.
拓展延伸:(3)如何过圆上一点,仅用没有刻度的直尺,作出已知直径的垂线?
已知: 如图,
如图, 是⊙
是⊙ 的直径,点
的直径,点 在⊙
在⊙ 上,求作:
上,求作: .
.
作法:①连接 ,
, ;
;
②在  上任取异于
上任取异于 、
、 的一点
的一点 ,连接
,连接 ,
, ;
;
③ 与
与 相交于
相交于 点,延长
点,延长 、
、 ,交于
,交于 点;
点;
④连接 、
、 并延长,交直径
并延长,交直径 于
于 ;
;
⑤连接 、
、 并延长,交⊙
并延长,交⊙ 于N.连接
于N.连接 . 则
. 则 .
.
请按上述作法在图④中作图,并说明 的理由.(提示:可以利用(2)中的结论)
的理由.(提示:可以利用(2)中的结论)
(1)同弧所对的圆周角相等, ,
, ,答案不唯一,如:
,答案不唯一,如: ;
;
(2) ,
, ,
, ,若四点组成的四边形对角互补,则这四点在同一圆上;
,若四点组成的四边形对角互补,则这四点在同一圆上;

(3)如图即为所作,理由见解析.

【解析】
试题分析:(1)根据题中所给的图,是非常熟悉的同弧所对的两个圆周角,故相等,后面两空可取特殊情况作判断,第四空可根据图①写出条件,但答案不唯一;(2)仿照(1)中对点 与圆的三种位置关系展开讨论,可以结合圆内接四边形对角互补得到图④的结论,后面两空同样可以取特殊情况判断;(3)按部就班作图不难,而在证明垂直过程中,根据提示要用到(2)的结论,即对角互补时四点共圆,故可结合圆的性质、圆内接四边形的性质、三角形中位线逆定理、平行线性质等予以证明.
与圆的三种位置关系展开讨论,可以结合圆内接四边形对角互补得到图④的结论,后面两空同样可以取特殊情况判断;(3)按部就班作图不难,而在证明垂直过程中,根据提示要用到(2)的结论,即对角互补时四点共圆,故可结合圆的性质、圆内接四边形的性质、三角形中位线逆定理、平行线性质等予以证明.
试题解析:(1)同弧所对的圆周角相等, ,
, ,答案不唯一,如:
,答案不唯一,如: ;
;
(2)如图即为所作.

此时 ,此时
,此时 ,此时
,此时 ;
;
(3)如图即为所作.


 是⊙
是⊙ 的直径,
的直径, 、
、 在⊙
在⊙ 上
上 
 ,
,
 点
点 是
是 三条高的交点
三条高的交点 

 ,
,
 点
点 、
、 、
、 、
、 在同一个圆上
在同一个圆上 

又 点
点 、
、 、
、 、
、 在⊙
在⊙ 上
上 
 ,
,






考点:1.分类讨论;几何作图;3. 圆的性质、圆内接四边形的性质、三角形中位线逆定理、平行线性质的综合应用.

 阅读快车系列答案
阅读快车系列答案 向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
向左平移1个单位,再向上平移3个单位得到的抛物线,其表达式为( )
 满足
满足 ,那么我们称这个方程为“凤凰”方程.已知方程
,那么我们称这个方程为“凤凰”方程.已知方程
 B.
B. C.
C. D.
D.
 x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
 ,以3为半径⊙O的同心圆与直线AB的位置关系是( )
,以3为半径⊙O的同心圆与直线AB的位置关系是( )  的图象交
的图象交 轴于
轴于 、
、 两点.
两点.
 的长;
的长; ,并写出当
,并写出当 与水平距离
与水平距离 之间的关系为
之间的关系为 ,由此可知铅球推出的距离是
,由此可知铅球推出的距离是  .
.
 ≥0,所以
≥0,所以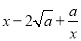 ≥0,从而
≥0,从而 (当
(当 时取等号).记函数
时取等号).记函数 ,由上述结论可知:当
,由上述结论可知:当 .
. ,则当x= 1 时,y1+y2取得最小值为 2 .
,则当x= 1 时,y1+y2取得最小值为 2 . ,求
,求 的最小值,并指出取得该最小值时相应的x的值.
的最小值,并指出取得该最小值时相应的x的值. B、
B、 C、
C、 D、
D、