题目内容
如下右图,直线y=﹣ x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .
x+4与x轴、y轴分别交于A、B两点,把△A0B绕点A顺时针旋转90°后得到△AO′B′,则点B′的坐标是 .

(7,3).
【解析】
试题分析:首先根据直线AB来求出点A和点B的坐标,B′的横坐标等于OA+OB,而纵坐标等于OA,进而得出B′的坐标.
试题解析:直线y=- x+4与x轴,y轴分别交于A(3,0),B(0,4)两点,
x+4与x轴,y轴分别交于A(3,0),B(0,4)两点,
∵旋转前后三角形全等,∠O′AO=90°,∠B′O′A=90°
∴OA=O′A,OB=O′B′,O′B′∥x轴,
∴点B′的纵坐标为OA长,即为3,
横坐标为OA+OB=OA+O′B′=3+4=7,
故点B′的坐标是(7,3).
考点:坐标与图形变化-旋转.

练习册系列答案
相关题目
 、
、 是方程
是方程 的两个实数根,不解方程,求下列代数式的值.
的两个实数根,不解方程,求下列代数式的值. ; (2)
; (2)
 的方程
的方程 是一元二次方程,则
是一元二次方程,则 的值为( ).
的值为( ). B.
B. C.
C. D.无解
D.无解  ㎝.则图中阴影部分的面积是 .
㎝.则图中阴影部分的面积是 .
 、
、 、
、 确定的圆为⊙
确定的圆为⊙ .
. 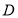 在线段
在线段 的同侧时,
的同侧时,
 ,理由是 ;
,理由是 ;
 ;
; ”、“
”、“ ”或“
”或“ ”);
”); 四点在同一个圆上的条件: .
四点在同一个圆上的条件: . 的异侧时的情形.
的异侧时的情形.
 如图,
如图, 的直径,点
的直径,点 .
. ,
, ;
; 上任取异于
上任取异于 ,
, ;
; 点,延长
点,延长 、
、 ,交于
,交于 点;
点; 于
于 ;
; . 则
. 则 .
. 年南京青奥会某项目
年南京青奥会某项目 名礼仪小姐的身高如下(单位:
名礼仪小姐的身高如下(单位: ):
): ,
, ,
, ,
, ,
,