题目内容
19.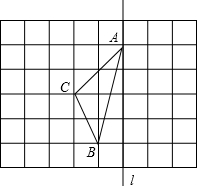 如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.
如图:在长度为1个单位的小正方形组成的网格中,点A、B、C在小正方形的顶点上.(1)在图中画出与△ABC关于直线l成轴对称的△AB′C′;
(2)△ABC的面积为3;
(3)在直线l上找一点P,使PB+PC的长最短,则这个最短长度为$\sqrt{13}$个单位长度.(在图形中标出点P)
分析 (1)先作出各点关于直线l的对称点,再顺次连接各点即可;
(2)利用矩形的面积减去三角形三个顶点上三角形的面积即可;
(3)连接BC′交直线l于点P,则P点即为所求点,根据勾股定理即可得出结论.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)S△ABC=2×4-$\frac{1}{2}$×2×1-$\frac{1}{2}$×2×2-$\frac{1}{2}$×4×1
=8-1-2-2
=3.
故答案为:3;
(3)如图所示,点P即为所求点,
PB+PC=BC′=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
故答案为:$\sqrt{13}$.
点评 本题考查的是轴对称-最短路线问题,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
9.已知一次函数y=x+m-3的图象与y轴的交点在x轴上方,则m需满足( )
| A. | m<3 | B. | m≤-3 | C. | m≥3 | D. | m>3 |
15.在一所有900名学生的学校随机调查了100人,其中有75人上学前吃早餐,在这所学校里随便问一个人,上学之前吃过早餐的概率是( )
| A. | $\frac{1}{9}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |

 画图题:画出此实物的三视图.
画图题:画出此实物的三视图. 如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F.
如图,已知AE=CF,AB∥DC,DE⊥AC于点E,BF⊥AC于点F. 已知:如图,AB∥ED,且AB=8cm,点F、点C在AD上,∠B=56°,∠E=56°,AF=DC=4cm,试求出DE的长.
已知:如图,AB∥ED,且AB=8cm,点F、点C在AD上,∠B=56°,∠E=56°,AF=DC=4cm,试求出DE的长.