Question

11．有一家苗圃计划植桃树和柏树，根据市场调查与预测，种植桃树的利润y₁（万元）与投资成本x（万元）满足如图①所示的二次函数y₁=ax²；种植柏树的利润y₂（万元）与投资成本x（万元）满足如图②所示的正比例函数y₂=kx．

（1）分别求出利润y₁（万元）和利润y₂（万元）关于投资成本x（万元）的函数关系式；
（2）如果这家苗圃以10万元资金投入种植桃树和柏树，桃树的投资成本不低于2万元且不高于8万元，苗圃至少获得多少利润？最多能获得多少利润？

Answer 1

分析 （1）利用待定系数法求两个函数的解析式；
（2）根据总投资成本为10万元，设种植桃树的投资成本x万元，总利润为W万元，则种植柏树的投资成本（10-x）万元，列函数关系式，发现是二次函数，画出函数图象，找出当2≤x≤8时的最小利润和最大利润．

解答 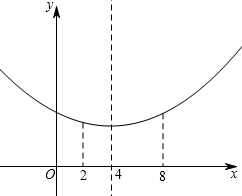解：（1）把（4，1）代入y₁=ax²中得：
16a=1，
a=$\frac{1}{16}$，
∴y₁=$\frac{1}{16}$x²，
把（2，1）代入y₂=kx中得：
2k=1，
k=$\frac{1}{2}$，
∴y₂=$\frac{1}{2}$x；
（2）设种植桃树的投资成本x万元，总利润为W万元，则种植柏树的投资成本（10-x）万元，
则W=y₁+y₂=$\frac{1}{16}$x²+$\frac{1}{2}$（10-x）=$\frac{1}{16}$（x-4）²+4，
由图象得：当2≤x≤8时，当x=4时，W有最小值，W_小=4，
当x=8时，W有最大值，W_大=$\frac{1}{16}$（8-4）2+4=5，
答：苗圃至少获得4万元利润，最多能获得5万元利润．

点评 本题是二次函数和一次函数的应用，考查了利用待定系数法求函数的解析式；对于二次函数，在求最值问题时，不一定都是顶点坐标，要根据实际情况和图象结合考虑，得出结论．