题目内容
13.下列命题中,原命题与逆命题均为真命题的有( )个.①若a≤0,则$\sqrt{{a}^{2}}$=-a;②全等三角形的面积相等;③两组对边分别相等的四边形是平行四边形;④对顶角相等;⑤直角三角形两条直角边的平方和等于斜边的平方.
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
分析 根据二次根式的化简法则、全等三角形的性质、平行四边形的判定、对顶角的性质、勾股定理等知识一一判断即可.
解答 解:①若a≤0,则$\sqrt{{a}^{2}}$=-a,原命题是真命题,逆命题是真命题.
②全等三角形的面积相等,原命题是真命题.逆命题是假命题.
③两组对边分别相等的四边形是平行四边形,原命题是真命题,逆命题是真命题.
④对顶角相等,原命题是真命题,逆命题是假命题.
⑤直角三角形两条直角边的平方和等于斜边的平方,原命题是真命题,逆命题是真命题
故①③⑤,
故选B.
点评 本题考查命题与定理,二次根式的化简法则、全等三角形的性质.平行四边形的判定、对顶角的性质、勾股定理等知识,解题的关键是熟练掌握基本概念,属于中考基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.下列调查中,适合采用全面调查方式的是( )
| A. | 对我县某学校某班50名同学体重情况的调查 | |
| B. | 对我县幸福河水质情况的调查 | |
| C. | 对我县某类烟花爆竹燃放安全情况的调查 | |
| D. | 对我县端午节期间市场上粽子质量情况的调查 |
4.平面直角坐标系中,点A在第四象限,点A到x轴的距离为2,到y轴的距离为3,则点A的坐标为( )
| A. | (2,-3) | B. | (-3,2) | C. | (3,-2) | D. | (-2,3) |
1. 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )
 如图,能判定EC∥AB的条件是( )
如图,能判定EC∥AB的条件是( )| A. | ∠B=∠ACB | B. | ∠B=∠ACE | C. | ∠A=∠ACE | D. | ∠A=∠ECD |
8.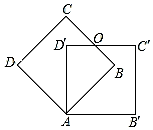 一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
 一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )
一顶点重合的两个大小完全相同的边长为3的正方形ABCD和正方形AB′C′D′,如图所示,∠DAD′=45°,边BC与D′C′交于点O,则四边形ABOD′的周长是( )| A. | 6 | B. | 6$\sqrt{2}$ | C. | 3$\sqrt{2}$ | D. | 3+3$\sqrt{2}$ |
18.为了解全校学生的视力状况,从1500名学生中抽出150名学生进行视力检测,这150名学生的视力是( )
| A. | 个体 | B. | 总体 | C. | 样本容量 | D. | 样本 |
5.要调查以下问题,适合采用普查的是( )
| A. | 了解一批圆珠笔芯的使用寿命 | |
| B. | 了解某班同学的视力情况 | |
| C. | 了解某种食品中某种添加剂的含量是否符合国家标准 | |
| D. | 了解某市居民对广场舞的认可度 |
2.点P(3,-4)关于y轴的对称点P′的坐标是( )
| A. | (-3,-4) | B. | (3,4) | C. | (-3,4) | D. | (-4,3) |