题目内容
10.某宾馆共有80个房间可供顾客居住.宾馆负责人根据前几年的经验作出预测:今年5月份,该宾馆每天的房间空闲数y(间)与每天的定价x(元/间)之间满足某个一次函数关系,且部分数据如表所示.| 每天的定价x(元/间) | 208 | 228 | 268 | … |
| 每天的房间空闲数y(间) | 10 | 15 | 25 | … |
(2)如果宾馆每天的日常运营成本为5000元,另外,对有顾客居住的房间,宾馆每天每间还需支出28元的各种费用,那么单纯从利润角度考虑,宾馆应将房间定价确定为多少时,才能获得最大利润?并请求出每天的最大利润.
分析 (1)待定系数法求出y关于x的一次函数解析式,令y=0求出x的值即可;
(2)根据:总利润=每个房间的利润×入住房间的数量-每日的运营成本,列出函数关系式,配方成顶点式后依据二次函数性质可得最值情况.
解答 解:(1)设y=kx+b,
由题意得:$\left\{\begin{array}{l}{208k+b=10}\\{228k+b=15}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{4}}\\{b=-42}\end{array}\right.$,
∴y=$\frac{1}{4}$x-42,
当y=0时,$\frac{1}{4}$x-42=0,
解得:x=168,
答:宾馆将每天的定价为168元/间时,所有的房间恰好被全部订完.
(2)设每天的利润为W元,根据题意,得:
W=(x-28)(80-y)-5000
=(x-28)[80-($\frac{1}{4}$x-42)]-5000
=-$\frac{1}{4}$x2+129x-8416
=-$\frac{1}{4}$(x-258)2+8225,
∵当x=258时,y=$\frac{1}{4}$×258-42=22.5,不是整数,
∴x=258舍去,
∴当x=256或x=260时,函数取得最大值,最大值为8224元,
答:宾馆应将房间定价确定为256或260元时,才能获得最大利润,最大利润为8224元.
点评 本题考查待定系数法求一次函数解析式及二次函数的实际应用,利用数学知识解决实际问题,解题的关键是建立函数模型,利用配方法求最值.

练习册系列答案
相关题目
16.据广东省旅游局统计显示,2016年4月全省旅游住宿设施接待过夜游客约27700000人,将27700000用科学记数法表示为( )
| A. | 0.277×107 | B. | 0.277×108 | C. | 2.77×107 | D. | 2.77×108 |
5.-2016的相反数是( )
| A. | $\frac{1}{2016}$ | B. | -2016 | C. | -$\frac{1}{2016}$ | D. | 2016 |
2. 如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )
如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )
 如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )
如图,边长相等的正方形、正六边形的一边重合,则∠1的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 35° |
 如图,已知AD=BC,AC=BD.
如图,已知AD=BC,AC=BD.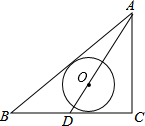 如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为$\frac{6}{7}$.
如图,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为$\frac{6}{7}$.
 如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.
如图,已知直线y=-x+3与x轴、y轴分别交于A,B两点,抛物线y=-x2+bx+c经过A,B两点,点P在线段OA上,从点O出发,向点A以1个单位/秒的速度匀速运动;同时,点Q在线段AB上,从点A出发,向点B以 $\sqrt{2}$个单位/秒的速度匀速运动,连接PQ,设运动时间为t秒.