题目内容
6．不等式$\frac{3x+13}{4}$＞$\frac{x}{3}$+2的解是x＞-3．分析 根据解一元一次不等式基本步骤：去分母、去括号、移项、合并同类项、系数化为1可得．
解答 解：去分母，得：3（3x+13）＞4x+24，
去括号，得：9x+39＞4x+24，
移项，得：9x-4x＞24-39，
合并同类项，得：5x＞-15，
系数化为1，得：x＞-3，
故答案为：x＞-3．
点评 本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．
练习册系列答案
相关题目
12．估计$\sqrt{19}$的值在（ ）
| A． | 2和3之间 | B． | 3和4之间 | C． | 4和5之间 | D． | 5和6之间 |
17．
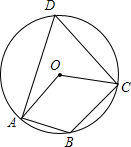如图所示，四边形ABCD是⊙O的内接四边形，若∠AOC=120°，则∠ABC的度数是（ ）
如图所示，四边形ABCD是⊙O的内接四边形，若∠AOC=120°，则∠ABC的度数是（ ）| A． | 100° | B． | 120° | C． | 140° | D． | 110° |
1．教练要从甲、乙两名射击运动员中选一名成绩较稳定的运动员参加比赛．两人在形同条件下各打了5发子弹，命中环数如下：甲：9、8、7、7、9；乙：10、8、9、7、6．应该选（ ）参加．
| A． | 甲 | B． | 乙 | C． | 甲、乙都可以 | D． | 无法确定 |
15．
如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为（ ）
如图，长4m的楼梯AB的倾斜角∠ABD为60°，为了改善楼梯的安全性能，准备重新建造楼梯，使其倾斜角∠ACD为45°，则调整后的楼梯AC的长为（ ）| A． | 2$\sqrt{3}$m | B． | 2$\sqrt{6}$m | C． | （2$\sqrt{3}$-2）m | D． | （2$\sqrt{6}$-2）m |
已知一包糖果共有5种颜色（糖果只有颜色差别），如图是这包糖果分布百分比的统计图，在这包糖果中任意取一粒，则取出糖果的颜色为绿色或棕色的概率是$\frac{1}{2}$．