题目内容
20．
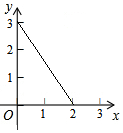如图，在平面直角坐标系中，有两点坐标分别为（2，0）和（0，3），则这两点之间的距离是（ ）| A． | $\sqrt{13}$ | B． | $\sqrt{5}$ | C． | 13 | D． | 5 |
分析 先根据A、B两点的坐标求出OA及OB的长，再根据勾股定理即可得出结论．
解答 
解：∵A（2，0）和B（0，3），
∴OA=2，OB=3，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$．
故选A．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
通城学典默写能手系列答案
相关题目
10．下列计算中，正确的是（ ）
| A． | （x3）4=x7 | B． | x3+x4=x7 | C． | （-x）3（-x）4=x7 | D． | x5÷x3=x2 |
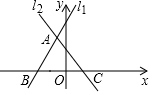如图直线l1：y=2x+4与直线l2：y=-2x+2相交于点A，且直线l1，l2分别交x轴于点B和C．
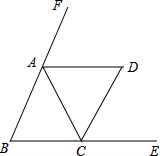如图，在△ABC中，AB=AC，AD、CD分别是△ABC的两个外角的平分线．