题目内容
15．
如图所示，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点．若四边形EFGH的面积为1，则矩形ABCD的面积是（ ）| A． | $\frac{5}{2}$ | B． | $\frac{5}{3}$ | C． | $\frac{3}{2}$ | D． | $\frac{15}{8}$ |
分析 设小正方形的边长a，那么矩形的面积=（S△AEF+S△BFG）×2+S四边形EFGH．
解答 解：设小正方形的边长a，那么矩形的面积=（S△AEF+S△BFG）×2+S四边形EFGH，
即：3a×5a=（2a×a÷2+a×4a÷2）×2+1，
9a2=1，
则a=$\frac{1}{3}$（a＞0），
故矩形的面积=3a×5a=$\frac{5}{3}$．
故选：B．
点评 此题主要考查了三角形面积求法，本题从矩形的面积表示方法入手进行计算是解题关键．
练习册系列答案
相关题目
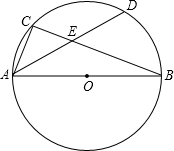如图，AB为⊙O的直径，C为⊙O上一点，弦AD平分∠BAC，交BC于点E，AB=10，AD=8，则AE的长为$\frac{7}{2}$．
如图，在四边形ABCD中，∠A=90°，AD=AB=4，BC=6，CD=2，求∠ADC的度数．
如图所示，点A在直线a外，点B在直线a上，在直线a上找一点P，使AP+BP最小的点P有1个，其位置是B点．
如图，在平面直角坐标系中，⊙A经过原点O，并且分别与x轴、y轴交于B、C两点，已知B（8，0），C（0，6），则⊙A的半径为（ ）
4．若a＞b，则下列结论正确的是（ ）
| A． | a2＞b2 | B． | a2＜b2 | ||
| C． | a2≥b2 | D． | a2与b2的大小关系不能确定 |