题目内容
10.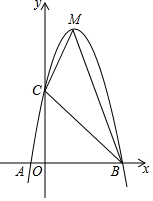 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.(1)求抛物线的解析式;
(2)求△MAB的面积.
分析 (1)设交点式y=a(x+1)(x-5),然后把C(0,5)代入求出a即可得到抛物线解析式;
(2)先把解析式配成顶点式,然后写出M点的坐标,再利用三角形面积公式求解.
解答 解:(1)设抛物线解析式为y=a(x+1)(x-5),
把C(0,5)代入得a•1•(-5)=5,解得a=-1,
所以抛物线解析式为y=-x2+4x+5;
(2)y=-x2+4x+5=-(x-2)2+9,则M(2,9)
所以△MAB的面积=$\frac{1}{2}$×(5+1)×9=27.
点评 本题考查了抛物线与x轴的交点:从二次函数的交点式:y=a(x-x1)(x-x2)(a,b,c是常数,a≠0)可直接得到抛物线与x轴的交点坐标(x1,0),(x2,0).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知a、b为实数,且$\sqrt{a-\frac{1}{2}}$+b2+4=4b,则a2015b2016的值是( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
1.下列计算正确的是( )
| A. | 3a+4b=7ab | B. | 7a-3a=4 | C. | 3a+a=3a2 | D. | 3a2b-2a2b=a2b |
15.正三角形的内切圆与外接圆的面积的比为( )
| A. | .1:3 | B. | 1:4 | C. | 1:2 | D. | 3:4 |
 在下面所示的方格纸中,
在下面所示的方格纸中, 如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为$2\sqrt{2}$cm,则CD的长为2cm.
如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为$2\sqrt{2}$cm,则CD的长为2cm.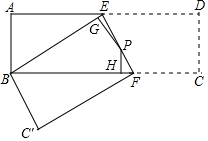 如图,长方形ABCD中,AB=3cm,AD=9cm,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的一点,PG⊥BE,PH⊥BF,则PG+PH=4.
如图,长方形ABCD中,AB=3cm,AD=9cm,将长方形ABCD沿EF折叠,使点D落在点B上,点C落在点C′处,点P为折痕EF上的一点,PG⊥BE,PH⊥BF,则PG+PH=4.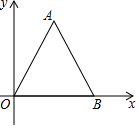 在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).