题目内容
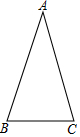
20.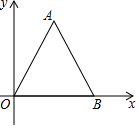 在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
在平面直角坐标系中,等边△AOB的位置如图,若OB=3,则点A的坐标为($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
分析 过点A作AC⊥OB于点C,根据△AOB是等边三角形,OB=3可得出OC=BC=$\frac{3}{2}$,∠OAC=$\frac{1}{2}$∠OAB=30°.在Rt△AOC中,根据∠OAC=30°,OA=2可得出AC及OC的长,进而得出A点坐标.
解答  解:过点A作AC⊥OB于点C,
解:过点A作AC⊥OB于点C,
∵△AOB是等边三角形,OB=2,
∴OC=BC=3,∠OAC=$\frac{1}{2}$∠OAB=30°,
在Rt△AOC中,
∵∠OAC=30°,OA=3,
∴OC=$\frac{3}{2}$,AC=OA•cos30°=3×$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{2}$,
∴A($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
故答案为A($\frac{3}{2}$,$\frac{3\sqrt{3}}{2}$).
点评 本题考查的是等边三角形的性质,熟知等边三角形三线合一的性质是解答此题的关键.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
10.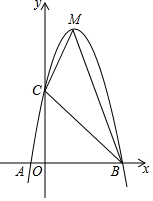 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MAB的面积.
 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.(1)求抛物线的解析式;
(2)求△MAB的面积.
11.下列代数式,书写符合规范的是( )
| A. | a×2 | B. | 2a2 | C. | $1\frac{1}{2}a$ | D. | (5÷3)a |
 如图,在△ABC中,AB=AC,∠ABC=70°.
如图,在△ABC中,AB=AC,∠ABC=70°.