题目内容
2. 如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为$2\sqrt{2}$cm,则CD的长为2cm.
如图,⊙O的半径为2cm,弦BC与弦AD交于点E,且∠CED=75°,弦AB为$2\sqrt{2}$cm,则CD的长为2cm.
分析 连接OA、OB、OC、OD、AC,根据勾股定理的逆定理得到∠AOB=90°,根据圆周角定理、三角形的外角的性质以及等边三角形的判定定理得到△COD是等边三角形,根据等边三角形的性质解答即可.
解答 解: 连接OA、OB、OC、OD、AC,
连接OA、OB、OC、OD、AC,
∵AB=$2\sqrt{2}$,OA=OB=2,
∴∠AOB=90°,
∴∠ACB=45°,
∴∠CAD=∠CED-∠ACB=30°,
∴∠COD=60°,
∴△COD是等边三角形,
∴CD=OC=2cm,
故答案为:2.
点评 本题考查的是圆周角定理、等边三角形的判定和性质,掌握同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
相关题目
10.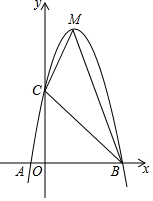 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
(1)求抛物线的解析式;
(2)求△MAB的面积.
 已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.
已知:如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),B点坐标为(5,0)点C(0,5),M为它的顶点.(1)求抛物线的解析式;
(2)求△MAB的面积.
11.下列代数式,书写符合规范的是( )
| A. | a×2 | B. | 2a2 | C. | $1\frac{1}{2}a$ | D. | (5÷3)a |
 如图,已知矩形ABCO的面积为8,反比例函数y=$\frac{k}{x}({k≠0})$的图象经过矩形ABCO对角线的交点E,则k=2.
如图,已知矩形ABCO的面积为8,反比例函数y=$\frac{k}{x}({k≠0})$的图象经过矩形ABCO对角线的交点E,则k=2.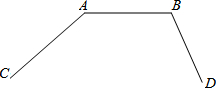 如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).
如图,已知三段公路(线段AB,以及射线AC、BD),请在AB的下方区域用尺规作一点P,使P点到三条公路的距离相等(保留作图痕迹,不写作法).