题目内容
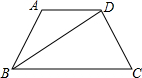 如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4| 3 |
A、4
| ||
| B、12 | ||
C、4
| ||
D、4
|
考点:梯形
专题:
分析:首先过点A作AF⊥BD于点F,过点D作DE⊥BC于点E,进而得出AD,DE的长,再利用梯形面积公式求出即可.
解答: 解:如图所示:过点A作AF⊥BD于点F,过点D作DE⊥BC于点E,
解:如图所示:过点A作AF⊥BD于点F,过点D作DE⊥BC于点E,
∵梯形ABCD中 AD∥BC,∠A=120°,
∴∠ABC=60°,∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠ADB=30°,
∴AB=AD,
∵BD=BC=4
,
∴BF=2
,
∴AB=AD=
=4,
可得:DE=
BD=2
,
故S梯形ABCD=
(AD+BC)×DE=
×(4+4
)×2
=4
+12.
故选:D.
 解:如图所示:过点A作AF⊥BD于点F,过点D作DE⊥BC于点E,
解:如图所示:过点A作AF⊥BD于点F,过点D作DE⊥BC于点E,∵梯形ABCD中 AD∥BC,∠A=120°,
∴∠ABC=60°,∠ADB=∠DBC,
∵BD平分∠ABC,
∴∠ABD=∠DBC=30°,
∴∠ABD=∠ADB=30°,
∴AB=AD,
∵BD=BC=4
| 3 |
∴BF=2
| 3 |
∴AB=AD=
| BF |
| cos30° |
可得:DE=
| 1 |
| 2 |
| 3 |
故S梯形ABCD=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
故选:D.
点评:此题主要考查了锐角三角函数关系以及梯形面积求法等知识,根据题意得出AD的长是解题关键.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
2100的个位数字是( )
| A、2 | B、4 | C、6 | D、8 |
 如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交BC于点E,交AD于点F,若四边形AECF恰好为菱形,则∠FOD=( )
如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交BC于点E,交AD于点F,若四边形AECF恰好为菱形,则∠FOD=( )| A、20° | B、30° |
| C、35° | D、15° |
20140的值是( )
| A、2014 | B、0 |
| C、1 | D、20140 |
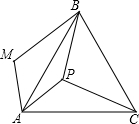 如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为
如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为 如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4.
如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4. 如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).
如图,M为等腰△ABD的底AB的中点,过D作DC∥AB,连结BC;AB=8cm,DM=4cm,DC=1cm,动点P自A点出发,在AB上匀速运动,动点Q自点B出发,在折线BC-CD上匀速运动,速度均为1cm/s,当其中一个动点到达终点时,它们同时停止运动,设点P运动t(s)时,△MPQ的面积为S(不能构成△MPQ的动点除外).