题目内容
 如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4.
如图,在?ABCD中,AB=5,AD=7,AE⊥BC于点E,AE=4.(1)求AC的长;
(2)△ACD的面积为
考点:平行四边形的性质,勾股定理
专题:
分析:(1)首先利用平行四边形的性质和勾股定理求出BE的长,进而得到CE的长,再利用勾股定理即可求出AC的长;
(2)根据平行四边形的性质可知:△ABC≌△ACD,所以△ACD的面积可转化求△ABC的面积,问题得解.
(2)根据平行四边形的性质可知:△ABC≌△ACD,所以△ACD的面积可转化求△ABC的面积,问题得解.
解答:解:(1)∵四边形ABCD是平行四边形,
∴BC=AD=7,
∵AE⊥BC于点E,AB=5,AE=4,
∴EB=
=3,
∴CE=BC-BE=4,
∴AC=
=4
;
(2)∵四边形ABCD是平行四边形,AC为对角线,
∴△ABC≌△ACD,
∴S△ABC=S△ACD=
×4×7=14,
故答案为:14.
∴BC=AD=7,
∵AE⊥BC于点E,AB=5,AE=4,
∴EB=
| AB2-AE2 |
∴CE=BC-BE=4,
∴AC=
| AE2+CE2 |
| 2 |
(2)∵四边形ABCD是平行四边形,AC为对角线,
∴△ABC≌△ACD,
∴S△ABC=S△ACD=
| 1 |
| 2 |
故答案为:14.
点评:此题主要考查平行四边形的性质和判定以及面积的计算以及勾股定理的运用,使学生能够灵活运用平行四边形的性质知识解决有关问题是此题考查的目的.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
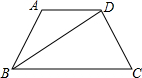 如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4| 3 |
A、4
| ||
| B、12 | ||
C、4
| ||
D、4
|
2014年2月14日,索契冬奥会速度滑冰女子1000米,中国名将张虹创造历史,滑出1分14秒02夺冠,拿下中国速度滑冰冬奥历史首金.在赛前的四组(每组10次)测试中,四组测试时间的平均数均为1分14秒03,方差分别为
=18.3,
=17.4,
=20.1,
=12.5.则这四组测试中最稳定的一组为( )
| s | 2 1 |
| s | 2 2 |
| s | 2 3 |
| s | 2 4 |
| A、第一组 | B、第二组 |
| C、第三组 | D、第四组 |
已知点(-6,y1),(8,y2)都在直线y=-
x-6上,则y1,y2大小关系是( )
| 1 |
| 2 |
| A、y1>y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、不能比较 |
 一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米.此后两人分别以另一速度匀速跑完全程,两人到达终点时均停止跑步,如图所示 的折线图表示了后一段路程中,两人之间的距离y(单位:米)与后一段路程跑步所用的时间x(秒)之间的关系,则这次越野赛跑的全程为
一次越野赛跑中,当小明跑了1600米时,小刚跑了1450米.此后两人分别以另一速度匀速跑完全程,两人到达终点时均停止跑步,如图所示 的折线图表示了后一段路程中,两人之间的距离y(单位:米)与后一段路程跑步所用的时间x(秒)之间的关系,则这次越野赛跑的全程为 如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=
如图,在平面直角坐标系中,动点P从原点O开始沿y轴的正方向运动,点B、C是一次函数y=k1x+b与反比例函数y=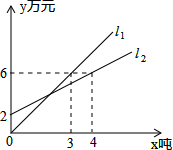 如图,l1反映了某产品的销售收入与销售量之间的关系,l2反映了该产品的销售城北与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.
如图,l1反映了某产品的销售收入与销售量之间的关系,l2反映了该产品的销售城北与销售量之间的关系,当销售收入大于销售成本时,该产品才开始盈利.