题目内容
 如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交BC于点E,交AD于点F,若四边形AECF恰好为菱形,则∠FOD=( )
如图,矩形ABCD中,AB=1,AC=2,对角线AC、BD相交于点O,直线EF过点O,交BC于点E,交AD于点F,若四边形AECF恰好为菱形,则∠FOD=( )| A、20° | B、30° |
| C、35° | D、15° |
考点:菱形的判定,矩形的性质
专题:
分析:由矩形的性质可得出OD=OC,判断出△DOC是等边三角形,再由菱形的对角线互相垂直可得出∠α的度数.
解答: 解:如图,∵在矩形ABCD中,AB=1,AC=2,
解:如图,∵在矩形ABCD中,AB=1,AC=2,
∴AB=CD=1,AC=BD=2
∴OD=OC=1,
∴OD=OC=DC,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵四边形AECF为菱形,
∴∠COF=90°,
∴∠α=90°-60°=30°.即∠FOD=30°.
故选:B.
 解:如图,∵在矩形ABCD中,AB=1,AC=2,
解:如图,∵在矩形ABCD中,AB=1,AC=2,∴AB=CD=1,AC=BD=2
∴OD=OC=1,
∴OD=OC=DC,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵四边形AECF为菱形,
∴∠COF=90°,
∴∠α=90°-60°=30°.即∠FOD=30°.
故选:B.
点评:本题考查的是矩形的性质、菱形的性质.此题利用了“矩形的对角线相等且相互平分”、“菱形的对角线互相垂直”的性质来解题的.

练习册系列答案
相关题目
下列关系式中,y为x的反比例函数的是( )
| A、xy=13 | ||
B、
| ||
| C、y=-x | ||
| D、y=x+1 |
一种细菌的直径是0.000016m,用科学记数法应记为( )
| A、1.6×10-7m |
| B、1.6×10-6m |
| C、1.6×10-5m |
| D、16×10-6m |
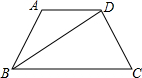 如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4
如图,已知梯形ABCD中 AD∥BC,BD平分∠ABC,∠A=120°,BD=BC=4| 3 |
A、4
| ||
| B、12 | ||
C、4
| ||
D、4
|
已知一次函数y=(m-4)x+2m+1的图象过一、二、四象限,则m的取值范围是( )
| A、m<4 | ||
B、m<-
| ||
C、-
| ||
| D、无解 |
已知点(-6,y1),(8,y2)都在直线y=-
x-6上,则y1,y2大小关系是( )
| 1 |
| 2 |
| A、y1>y2 |
| B、y1=y2 |
| C、y1<y2 |
| D、不能比较 |
 直角三角形在正方形网格纸中的位置如图,则tanα=
直角三角形在正方形网格纸中的位置如图,则tanα=