题目内容
2.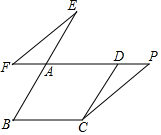 如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.
如图,在平行四边形ABCD中,延长BA至点E,使AE=AB,点F、P在边AD所在的直线上,EF∥CP.(1)求证:DF-DP=BC;
(2)的条件下,若CD=15,EF=20,tan∠AFE=$\frac{3}{4}$,BC=14,求DF的长.
分析 (1)证出∠EAF=∠CDP,∠F=∠P,由AAS证明△AEF≌△DCP,得出DP=AF,即可得出结论;
(2)过点E作EG⊥AD于点G,与平行四边形的性质得出AE=AB=CD=15,AD=BC=14,由三角函数求出EG=12,FG=16,由勾股定理求出AG=9,得出AF=7,即可得出DF的长.
解答 (1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,
∴∠BAF=∠CDA,
∴180°-∠BAF=180°-∠CDA,
∴∠EAF=∠CDP,
∵AE=AB,
∴AE=DC,
∵EF∥CP,
∴∠F=∠P,
在△AEF和△DCP中,$\left\{\begin{array}{l}{∠EAF=∠CDP}&{\;}\\{∠F=∠P}&{\;}\\{AE=DC}&{\;}\end{array}\right.$,
∴△AEF≌△DCP(AAS),
∴DP=AF,
∵DF-AF=AD,
∴DF-DP=BC;
(2)过点E作EG⊥AD于点G,如图所示:
∵四边形ABCD是平行四边形,
∴AE=AB=CD=15,AD=BC=14,
在Rt△EFG中,tan∠AFE=$\frac{EG}{FG}$=$\frac{3}{4}$,
∴sin∠AFE=$\frac{EG}{EF}$=$\frac{3}{5}$,cos∠AFE=$\frac{4}{5}$,
∴EG=sin∠AFE×EF=$\frac{3}{5}$×20=12,FG=cos∠AFE×EF=$\frac{4}{5}$×20=16,
∴在Rt△EFG中,由勾股定理得:AG═$\sqrt{1{5}^{2}-1{2}^{2}}$=9,
∴AF=FG-AG=16-9=7,
∴DF=AF+AD=7+14=21.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;熟练掌握平行四边形的性质,并能进行推理论证是解决问题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
| A. | 平均数是1 | B. | 众数是1 | C. | 中位数是1 | D. | 极差是4 |
 如图,直线y=ax与双曲线y=$\frac{k}{x}$(x>0)交于点A(1,2),则不等式ax>$\frac{k}{x}$的解集是x>1.
如图,直线y=ax与双曲线y=$\frac{k}{x}$(x>0)交于点A(1,2),则不等式ax>$\frac{k}{x}$的解集是x>1.
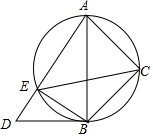 将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC.
 如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.
如图,在平面直角坐标系中,圆M经过原点O,直线y=-$\frac{3}{4}$x-6与x轴、y轴分别相交于A,B两点.