题目内容
3.古希腊数学家把1、3、6、10、15、21、…叫做三角形数,其中1是第一个三角形数,3是第二个三角形数,6是第三个三角形数,…,依此类推,第100个三角形数是5050.分析 设第n个三角形数为an,分析给定的三角形数,根据数的变化找出变化规律“an=1+2+…+n=$\frac{n(n+1)}{2}$”,依此规律即可得出结论.
解答 解:设第n个三角形数为an,
∵a1=1,
a2=3=1+2,
a3=6=1+2+3,
a4=10=1+2+3+4,
…
∴an=1+2+…+n=$\frac{n(n+1)}{2}$,
将n=100代入an,得:a100=$\frac{100(100+1)}{2}$=5050,
故答案为:5050.
点评 本题考查了规律型中的数字的变化类,解题的关键是找出变化规律“an=1+2+…+n=$\frac{n(n+1)}{2}$”.

练习册系列答案
相关题目
14.下列关于正方形的叙述,正确的是( )
| A. | 正方形有且只有一个内切圆 | |
| B. | 正方形有无数个外接圆 | |
| C. | 对角线相等且垂直的四边形是正方形 | |
| D. | 用一根绳子围成一个平面图形,正方形的面积最大 |
8.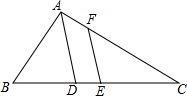 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
 如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )
如图,△ABC中,E是BC中点,AD是∠BAC的平分线,EF∥AD交AC于F.若AB=11,AC=15,则FC的长为( )| A. | 11 | B. | 12 | C. | 13 | D. | 14 |
12.对一组数据:-2,1,2,1,下列说法不正确的是( )
| A. | 平均数是1 | B. | 众数是1 | C. | 中位数是1 | D. | 极差是4 |

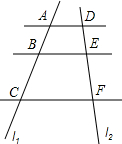 如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A、B、C和点D、E、F.若AB=2,BC=4,则$\frac{DE}{DF}$的值为$\frac{1}{3}$.
如图,直线AD∥BE∥CF,它们分别交直线l1、l2于点A、B、C和点D、E、F.若AB=2,BC=4,则$\frac{DE}{DF}$的值为$\frac{1}{3}$. 已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).
已知:如图,直线y=ax+b与双曲线y=$\frac{k}{x}$(x>0)相交于点A(2,3)和点B(6,m).