题目内容
若|b﹣1|+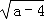 =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
=0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
k≤4且k≠0 .
【考点】根的判别式;非负数的性质:绝对值;非负数的性质:算术平方根.
【分析】根据非负数的性质求出a、b的值,转化成关于k的不等式即可解答.
【解答】解:∵|b﹣1|+ =0,
=0,
∴b=1,a=4,
∴原方程为kx2+4x+1=0,
∵该一元二次方程有实数根,
∴△=16﹣4k≥0,
解得:k≤4,
∵方程kx2+ax+b=0是一元二次方程,
∴k≠0,
k的取值范围是:k≤4且k≠0,
故答案为:k≤4且k≠0.
【点评】本题考查了根的判别式,利用判别式得到关于k的不等式是解题的关键.

练习册系列答案
相关题目
 出一个代数恒等式是( )
出一个代数恒等式是( )
 (2)求证:△ADE是直角三角形;
(2)求证:△ADE是直角三角形;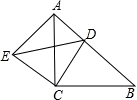
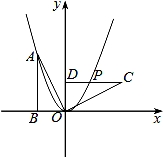



 B.
B. C.
C. D.
D. ;
;