题目内容
如图将4个长、宽分别均为a,b的长方形,摆成了一个大的正方形,利用面积的不同表示方法写 出一个代数恒等式是( )
出一个代数恒等式是( )

A.a2+2ab+b2=(a+b)2 B.a2﹣2ab+b2=(a﹣b)2
C.4ab=(a+b)2﹣(a﹣b)2 D.(a+b)(a﹣b)=a2﹣b2
C【考点】完全平方公式的几何背景.
【分析】根据图形的组成以及正方形和长方形的面 积公式,知:大正方形的面积﹣小正方形的面积=4个矩形的面积.
积公式,知:大正方形的面积﹣小正方形的面积=4个矩形的面积.
【解答】解:∵大正方形的面积﹣小正方形的面积=4个矩形的面积,
∴(a+b)2﹣(a﹣b)2=4ab,即4ab=(a+b)2﹣(a﹣b)2.
故选C.
【点评】考查了完全平方公式的几何背景,能够正确找到大正方形和小正方形的边长是难点.解决问题的关键是读懂题意,找到所求的量的等量关系.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
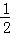 ,y1)和(2,y2)都在抛物线上,那么y1<y2;
,y1)和(2,y2)都在抛物线上,那么y1<y2;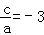 ;
;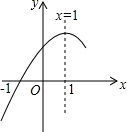

 =160°,∠D=4∠C,求四边形ABCD各内角的度数.
=160°,∠D=4∠C,求四边形ABCD各内角的度数.

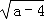 =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
=0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 . B.y=
B.y= C.y=
C.y= D.y=
D.y=