题目内容
.已知AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.
(1)如图①,若AB=2,∠P=30°,求AP的长(结果保留根号);
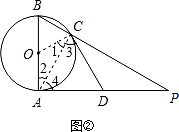
(2)如图②,若D为AP的中点,求证:直线CD是⊙O的切线.
【考点】切线的判定与性质;勾股定理.
【专题】计算题;证明题.
【分析】(1)易证PA⊥AB,再通过解直角三角形求解;
(2)本题连接OC,证出OC⊥CD即可.首先连接AC,得出直角三角形ACP,根据直角三角形斜边上中线等于斜边一半得CD=AD,再利用等腰三角形性质可证∠OCD=∠OAD=90°,从而解决问题.
【解答】解:(1)∵AB是⊙O的直径,AP是切线,
∴∠BAP=90°.
在Rt△PAB中,AB=2,∠P=30°,
∴BP=2AB=2×2=4.
由勾股定理,得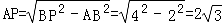 .
.
(2)如图,连接OC、AC.
∵AB是⊙O的直径,
∴∠BCA=90°,又∵∠ACP=180°﹣∠BCA=90°.
在Rt△APC中,D为AP的中点,
∴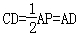 .
.
∴∠4=∠3.
又∵OC=OA,
∴∠1=∠2.
∵∠2+∠4=∠PAB=90°,
∴∠1+∠3=∠2+∠4=90°.
即OC⊥CD.
∴直线CD是⊙O的切线.
【点评】此题考查了切线的判定和性质及解直角三角形等知识点,难度适中.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则不等式2x≥ax+4的解集为( )
|
| A. | x≥ | B. | x≤3 | C. | x≤ | D. | x≥3 |


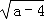 =0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .
=0,且一元二次方程kx2+ax+b=0有实数根,则k的取值范围是 .


 B.y=
B.y= C.y=
C.y= D.y=
D.y=