题目内容
3.在平行四边形中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,则平行四边形ABCD的周长等于12或20.分析 根据题意分别画出图形,BC边上的高在平行四边形的内部和外部,进而利用勾股定理求出即可.
解答 解:如图1所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,AB=CD=5,
BE=$\sqrt{A{B}^{2}-A{E}^{2}}$=3,
∴AD=BC=5,
∴?ABCD的周长等于:20,
如图2所示:
∵在?ABCD中,BC边上的高为4,AB=5,AC=2$\sqrt{5}$,
∴EC=$\sqrt{A{C}^{2}-A{E}^{2}}$=2,AB=CD=5,
BE=3,
∴BC=3-2=1,
∴?ABCD的周长等于:1+1+5+5=12,
综上所述:?ABCD的周长等于12或20.
故答案为:12或20.
点评 此题主要考查了平行四边形的性质以及勾股定理等知识,利用分类讨论得出是解题关键.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
12.已知菱形ABCD的对角线AC,BD的长度是关于x的方程x2-14x+48=0的两个实数根,则此菱形的面积是( )
| A. | 20 | B. | 24 | C. | 48 | D. | 不确定 |
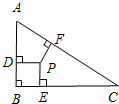 如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( )
如图,△ABC中,∠B=90°,两直角边AB=3,BC=4,AC=5.三角形内有一点P到各边的距离相等,则这个距离为( ) 如图,直线y1=x+2与双曲线y2=$\frac{k}{x}$交于A(a,4),B(m,n).
如图,直线y1=x+2与双曲线y2=$\frac{k}{x}$交于A(a,4),B(m,n). 如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=7.
如图,AD∥BC,AB⊥BC于点B,AD=4,将CD绕点D逆时针旋转90°至DE,连接AE、CE,若△ADE的面积为6,则BC=7.