题目内容
10. 如图,正方形ABCD中,AB=$\sqrt{3}$,延长BC至E,使BE=BD,则△BDE的面积为$\frac{3}{2}$$\sqrt{2}$.
如图,正方形ABCD中,AB=$\sqrt{3}$,延长BC至E,使BE=BD,则△BDE的面积为$\frac{3}{2}$$\sqrt{2}$.
分析 根据正方形的性质得出BD=$\sqrt{6}$,进而根据BE=BD,再计算出△BDE的面积即可.
解答 解:∵四边形ABCD是正方形,AB=$\sqrt{3}$,
∴BD=BE=$\sqrt{6}$,
∴△BDE的面积=$\frac{1}{2}$$\sqrt{6}$×$\sqrt{3}$=$\frac{3}{2}$$\sqrt{2}$,
故答案为:$\frac{3}{2}\sqrt{2}$.
点评 本题考查了正方形的性质,三角形面积的计算,熟记各性质并准确识图是解题的关键.

练习册系列答案
相关题目
16.一组数据6、4、a、3、2的平均数是4,则这组数据的方差为( )
| A. | 0 | B. | 2 | C. | $\sqrt{2}$ | D. | 10 |
14.下列运算结果正确的是( )
| A. | -87×(-83)=7221 | B. | -2.68-7.42=-10 | C. | 3.77-7.11=-4.66 | D. | $\frac{-101}{102}<\frac{-102}{103}$ |
5.在解方程:$\frac{x+1}{2}-\frac{x-1}{3}=1$时,去分母正确的是( )
| A. | 3x+1-2x-1=1 | B. | 3x+1-2X-1=6 | C. | 3(x+1)-2(x-1)-=1 | D. | 3(x+1)-2(x-1)=6 |

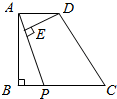 如图:在四边形ABCD中,AD∥BC,∠B=90°,AD=1,AB=$\frac{3}{2}$,BC=2,P是BC边上的一个动点(P与点B不重合,可以与点C重合).DE⊥AP于点E.设AP=x,DE=y,求y关于x的函数表达式和自变量x的取值范围.
如图:在四边形ABCD中,AD∥BC,∠B=90°,AD=1,AB=$\frac{3}{2}$,BC=2,P是BC边上的一个动点(P与点B不重合,可以与点C重合).DE⊥AP于点E.设AP=x,DE=y,求y关于x的函数表达式和自变量x的取值范围.