题目内容

15．已知点A（1，-k2+2）在有最高点的抛物线y=kx2上，求常数k的值．

分析 先根据抛物线有最高点判断出k＜0，然后将点A的坐标代入抛物线解析式解关于k的一元二次方程即可．

解答 解：∵抛物线y=kx2有最高点，
∴k＜0，
∵点A（1，-k2+2）在抛物线上，
∴-k2+2=k，
整理得，k2+k-2=0，
解得k1=1（舍去），k2=-2，
所以，常数k的值是-2．

点评 本题考查了二次函数的最值问题，二次函数图象上点的坐标特征，判断出k＜0是解题的关键．

练习册系列答案
相关题目
5．下列各曲线中，不能表示y是x的函数的是（　　）
A．B．C．D．
6．已知⊙O的直径为$\sqrt{2}$cm，点A在⊙O上，则线段OA的长为$\frac{\sqrt{2}}{2}$cm．
3．矩形ABCD中，对角线AC和BD相交于O，∠AOB=60°，AC=10，
（1）求AB；
（2）求AD；
（3）求矩形ABCD的面积．
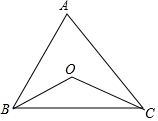10．如图，△ABC中，∠ABC与∠ACB的角平分线交于点O，若∠BAC=82°，则∠BOC=131°．
20．计算：
（1）（-3$\frac{2}{3}$）-（-2.4）+（-$\frac{1}{3}$）-（+4$\frac{2}{5}$）                        
（2）1÷（1$\frac{1}{6}$-8$\frac{3}{4}$×$\frac{2}{7}$）+$\frac{7}{18}$÷$\frac{14}{27}$
（3）-32×（-$\frac{1}{2}$）3-（$\frac{3}{4}$+$\frac{1}{6}$-$\frac{3}{8}$）÷（-$\frac{1}{24}$）                     
（4）（-1）4-{$\frac{3}{5}$-[（$\frac{1}{3}$）2+0.4×（-1$\frac{1}{2}$）]÷（-2）2}．
7．计算：$\sqrt{2}$（2-$\sqrt{6}$）+2$\sqrt{3}$．
4．如图一次函数y=kx+b的图象进过点A点B，求此函数的表达式．
18．观察下列式：71=7，72=49，73=343，74=2041，75=16807，76=117649，…根据上述算式中的规律，你认为72018的末位数字是（　　）
A．9B．7C．3D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网