题目内容
 如图所示,已知AB为⊙O的直径,半径OC⊥AB,E为OB上一点,弦AD⊥CE交OC于点F,猜想OE与OF的数量关系,并说明你的理由.
如图所示,已知AB为⊙O的直径,半径OC⊥AB,E为OB上一点,弦AD⊥CE交OC于点F,猜想OE与OF的数量关系,并说明你的理由.考点:全等三角形的判定与性质
专题:
分析:由垂直的性质就可以得出∠AFO=∠CEO,由圆的性质就可以得出AO=CO,进而得出△AOF≌△COE,就可以得出结论.
解答:解:OE=OF.
理由:∵OC⊥AB,
∴∠AOC=∠COE=90°.
∴∠C+∠CEO=90°
∵AD⊥CE,
∴∠FGC=90°,
∴∠C+∠CFG=90°,
∴∠CFG=∠CEO.
∵∠AFO=CFO,
∴∠AFO=∠CEO.
在△AOF和△COE中,
,
∴△AOF≌△COE(AAS),
∴OF=OE.
理由:∵OC⊥AB,
∴∠AOC=∠COE=90°.
∴∠C+∠CEO=90°
∵AD⊥CE,

∴∠FGC=90°,
∴∠C+∠CFG=90°,
∴∠CFG=∠CEO.
∵∠AFO=CFO,
∴∠AFO=∠CEO.
在△AOF和△COE中,
|
∴△AOF≌△COE(AAS),
∴OF=OE.
点评:本题考查了圆的性质的运用,直角三角形的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
相关题目
 如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥的高是( )
如图,已知圆锥侧面展开图的扇形面积为65π cm2,扇形的弧长为10π cm,则圆锥的高是( )| A、5cm | B、10cm |
| C、12cm | D、13cm |
 有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )
有理数a,b在数轴上的位置如图所示,则下列判断正确的是( )| A、ab>0 | ||
B、
| ||
| C、a<b | ||
| D、a>0>b |
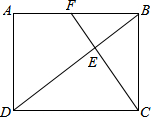 如图,在矩形ABCD中,CF⊥BD于点E,交AB于点F,如果F是AB的中点,则AD:AB=
如图,在矩形ABCD中,CF⊥BD于点E,交AB于点F,如果F是AB的中点,则AD:AB= 尺规作图:(不写作法,保留作图痕迹)已知线段a、b和∠α.
尺规作图:(不写作法,保留作图痕迹)已知线段a、b和∠α.
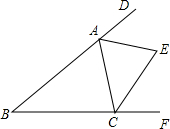 如图所示,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为
如图所示,在△ABC中,∠B=48°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC的度数为