题目内容
如图，已知E是正方形ABCD中DC边延长线上一点，连接AE交BC于点F，∠BCE的平分线交BE于点G，连接FG，求证：AB∥FG．考点：平行线分线段成比例
专题：证明题
分析：根据正方形性质得出AB=BC，AB∥CD，根据平行线分线段成比例定理得出比例式，根据角平分线性质得出比例式，即可推出
=
，即可得出答案．
| EF |
| AF |
| EG |
| BG |
解答：证明：∵四边形ABCD是正方形，
∴AB=BC，AB∥CD，
∴△ECF∽△ABF，
∴
=
，
∵CG平分∠BCE，
∴
=
，
∴
=
，
∴
=
，
∵∠FEG=∠AEB，
∴△FEG∽△AEB，
∴∠EFG=∠EAB，
∴FG∥AB．
∴AB=BC，AB∥CD，
∴△ECF∽△ABF，
∴
| EC |
| AB |
| EF |
| AF |
∵CG平分∠BCE，
∴
| EC |
| BC |
| EG |
| BG |
∴
| EF |
| AF |
| EG |
| BG |
∴
| FE |
| AE |
| EG |
| BE |
∵∠FEG=∠AEB，
∴△FEG∽△AEB，
∴∠EFG=∠EAB，
∴FG∥AB．
点评：本题考查了相似三角形的性质和判定，平行线分线段成比例定理的应用，主要考查学生的推理能力，解此题的关键是求出
=
．
| EF |
| AF |
| EG |
| BG |
练习册系列答案
名校课堂系列答案
相关题目
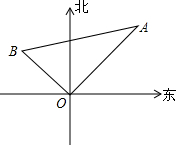如图所示，甲渔船以8海里/时的速度离开港口O向东北方向航行，乙渔船以6海里/时的速度离开港口O向西北方向航行，他们同时出发，一个半小时后，甲、乙两渔船相距多少海里？
如图，在△ABC中，E为AC的中点，F在AB上，且