题目内容
 如图,线段BD=
如图,线段BD=| 1 |
| 3 |
| 1 |
| 4 |
考点:两点间的距离
专题:
分析:设BD=x,则AB=3x,CD=4x,所以BC=CD-BD=3x,所以AC=AB+BC=6x,然后由MN=10,可以求出x的值,即可求出AC的值.
解答:解:∵线段BD=
AB=
CD,
设BD=xcm,则AB=3xcm,CD=4xcm,
∴BC=CD-BD=3xcm,
∴AC=AB+BC=6xcm,
∵点M、N分别是线段AB、CD的中点,
∴AM=
AB=1.5xcm,NC=
CD=2xcm,
∵MN=AC-AM-NC=6x-1.5x-2x=2.5xcm,
且MN=10cm,
∴2.5x=10,
∴x=4,
∴AC=6x=24cm

| 1 |
| 3 |
| 1 |
| 4 |
设BD=xcm,则AB=3xcm,CD=4xcm,
∴BC=CD-BD=3xcm,
∴AC=AB+BC=6xcm,
∵点M、N分别是线段AB、CD的中点,
∴AM=
| 1 |
| 2 |
| 1 |
| 2 |
∵MN=AC-AM-NC=6x-1.5x-2x=2.5xcm,
且MN=10cm,
∴2.5x=10,
∴x=4,
∴AC=6x=24cm

点评:此题考查了两点间的距离,解题关键是:设BD=x,然后将其他线段用x表示.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
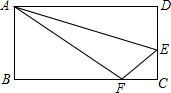 如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度.
如图,折叠长方形纸片ABCD,使点D落在边BC上的点F处,折痕为AE,AB=CD=6,AD=BC=10,试求EC的长度. 如图所示,已知点B,C,D在一条直线上,BC=AC,CD=CE,∠2=∠3=55°,则∠1=
如图所示,已知点B,C,D在一条直线上,BC=AC,CD=CE,∠2=∠3=55°,则∠1=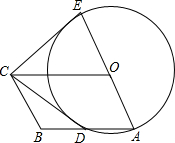 如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,
如图,四边形OABC是平行四边形,以O为圆心,OA为半径的圆交AB于D,延长AO交⊙O于E,连接CD,CE,若CE是⊙O的切线,