Question

10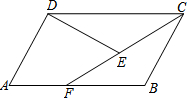．在平行四边形ABCD中，点F为边AB上一点，且CD=CF，AF=EF，连结D、E．求证：DE=BC．

Answer 1

分析 根据平行四边形的性质可得CD=AB，CD∥AB，利用平行线的性质可得∠DCE=∠BCF，再由条件AF=EF可得CE=BF，再利用SAS判定△DEC≌△CBF，进而可得DE=BC．

解答 证明：∵四边形ABCD是平行四边形，
∴CD=AB，CD∥AB，
∴∠DCE=∠BCF，
∵CD=AB，CD=CF，
∴AB=CF，
∵AF=EF，
∴BF=CE，
在△DEC和△CBF中$\left\{\begin{array}{l}{CD=CF}\\{∠DCE=∠CFB}\\{CE=FB}\end{array}\right.$，
∴△DEC≌△CBF（SAS），
∴DE=BC．

点评 此题主要考查了平行四边形的性质和全等三角形的判定和性质，关键是掌握平行四边形的对边相等且平行．