题目内容
5．
如图，正方形网格中每个小正方形边长都是1．（1）在直线l上找一点P，使PB+PC的值最小；
（2）连接PA、PC，计算四边形PABC的面积；
（3）若图中的格点Q到直线BC的距离等于$\sqrt{2}$，则图中所有满足条件的格点Q有16个．
分析 （1）找到B点对称点B′，再连接B′C交直线l于点P，即可得出答案；
（2）直接将四边形分割为两个三角形，进而求出其面积；
（3）利用勾股定理结合网格得出平行于直线BC且到直线BC的距离为$\sqrt{2}$的直线，即可得出答案．
解答 
解：（1）如图所示：点P即为所求；
（2）四边形PABC的面积为：$\frac{1}{2}$×3×5+$\frac{1}{2}$×4×1=9.5；
（3）图中所有满足条件的格点Q有：16个．
故答案为：16．
点评 此题主要考查了轴对称-求最短路线以及点到直线的距离等知识，正确得出P点位置是解题关键．
练习册系列答案
相关题目
如图，直线y=kx+b与双曲线y=$\frac{m}{x}$交于点A（n，-2），B（2，1）．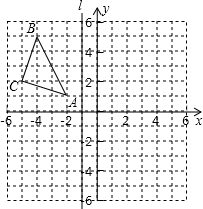
如图，△ABC在平面直角坐标系中，点A、B、C的坐标分别为A（-2，1），B（-4，5），C（-5，2），直线l经过点（-1，0）且和y轴平行．
如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交$\widehat{BC}$于D．