题目内容
3.用配方法解方程:(1)x2-2x=5
(2)x2-$\sqrt{3}$x-2=0;
(3)4x2-6x-4=0
(4)-$\frac{1}{2}{{x}^{2}}$+3x=$\frac{9}{2}$.
分析 (1)先配方,再开方,即可得出两个一元一次方程,求出方程的解即可;
(2)移项后配方,再开方,即可得出两个一元一次方程,求出方程的解即可;
(3)移项后配方,再开方,即可得出两个一元一次方程,求出方程的解即可;
(4)去分母后配方,再开方,即可得出两个一元一次方程,求出方程的解即可.
解答 解:(1)x2-2x=5,
配方得:x2-2x+1=5+1,
(x-1)2=6,
x-1=$±\sqrt{6}$,
x1=1+$\sqrt{6}$,x2=1-$\sqrt{6}$;
(2)x2-$\sqrt{3}$x-2=0,
x2-$\sqrt{3}$x=2,
配方得:x2-$\sqrt{3}$x+($\frac{\sqrt{3}}{2}$)2=2+($\frac{\sqrt{3}}{2}$)2
(x-$\frac{\sqrt{3}}{2}$)2=$\frac{11}{4}$,
x-$\frac{\sqrt{3}}{2}$=$±\frac{\sqrt{11}}{2}$,
x1=$\frac{\sqrt{3}+\sqrt{11}}{2}$,x2=$\frac{\sqrt{3}-\sqrt{11}}{2}$;
(3)4x2-6x-4=0,
4x2-6x=4,
x2-$\frac{3}{2}$x=1,
配方得:x2-$\frac{3}{2}$x+($\frac{3}{4}$)2=1+($\frac{3}{4}$)2,
(x-$\frac{3}{4}$)2=$\frac{25}{16}$,
x-$\frac{3}{4}$=±$\frac{5}{4}$,
x1=2,x2=-$\frac{1}{2}$;
(4)-$\frac{1}{2}{{x}^{2}}$+3x=$\frac{9}{2}$,
x2-6x=-9,
配方得:x2-6x+9=-9+9,
(x-3)2=0,
x-3=0,
x=3,
即x1=x2=3.
点评 本题考查了解一元二次方程的应用,解此题的关键是能正确配方,题目是一道比较常见的题目,难度不是很大.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. |  | B. |  | C. |  | D. |  |
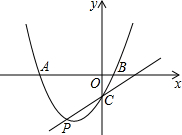 如图,抛物线$y=\frac{1}{2}{x^2}+mx+n$交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1.
如图,抛物线$y=\frac{1}{2}{x^2}+mx+n$交x轴于A、B两点,交y轴于点C,点P是它的顶点,点A的横坐标是-3,点B的横坐标是1. 如图,⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上一点,则∠CPB=65°.
如图,⊙O是△ABC的外接圆,∠CAB=65°,P是⊙O上一点,则∠CPB=65°.