题目内容
13.在反比例函数y=-$\frac{{m}^{2}+1}{x}$的图象上有三点A(-2,y1)、B(-1,y2)、C(1,y3),比较y1,y2,y3的大小y3<y1<y2.分析 先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再由各点横坐标的值即可得出结论.
解答 解:∵反比例函数y=-$\frac{{m}^{2}+1}{x}$中,k=-(m2+1)<0,
∴函数图象的两个分支分别位于二四象限,且在每一象限内,y随x的增大而增大.
∵-2<-1<0,1>0,
∴点A(-2,y1),B(-1,y2)在第二象限,点C(1,y3)在第四象限,
∴y3<y1<y2.
故答案为:y3<y1<y2.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
1.在(-1)2016、-12015、-22、(-3)2这四个数中,最大的数比最小的数要大( )
| A. | 13 | B. | 10 | C. | 8 | D. | 5 |
18.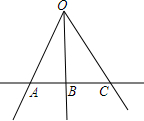 如图,下列说法正确的是( )
如图,下列说法正确的是( )
 如图,下列说法正确的是( )
如图,下列说法正确的是( )| A. | 图中共有5条线段 | B. | 直线AB与直线AC是指同一条直线 | ||
| C. | 射线AB与射线BA是指同一条射线 | D. | 点O在直线AC上 |
 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.
如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.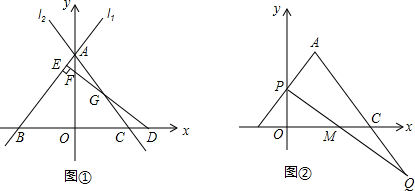
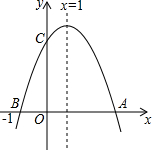 如图二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①OA=3;②a+b+c<0;③abc>0;④b2-4ac>0;⑤2a+b=0.其中正确的结论个数是( )个.
如图二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①OA=3;②a+b+c<0;③abc>0;④b2-4ac>0;⑤2a+b=0.其中正确的结论个数是( )个.