题目内容
3.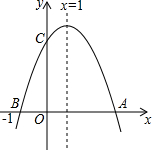 如图二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①OA=3;②a+b+c<0;③abc>0;④b2-4ac>0;⑤2a+b=0.其中正确的结论个数是( )个.
如图二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于点C,点B坐标(-1,0),下面的四个结论:①OA=3;②a+b+c<0;③abc>0;④b2-4ac>0;⑤2a+b=0.其中正确的结论个数是( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据点B坐标和对称轴求出A的坐标,即可判断①;由图象可知:当x=1时,y>0,把x=1代入二次函数的解析式,即可判断②;抛物线的开口向下,对称轴在y轴右侧,与y轴的交点在y轴的正半轴上,得出a<0,b>0,c>0,即可判断③;根据抛物线与x轴有两个交点,即可判断④,根据对称轴x=-$\frac{b}{2a}$=1,得2a+b=0,即可判断⑤.
解答 解:∵点B坐标(-1,0),对称轴是直线x=1,
∴A的坐标是(3,0),
∴OA=3,∴①正确;
∵由图象可知:当x=1时,y>0,
∴把x=1代入二次函数的解析式得:y=a+b+c>0,∴②错误;
∵抛物线开口向下,a<0,对称轴在y轴右侧,b>0,与y轴交于正半轴,c>0,
∴abc<0,③错误;
∵抛物线与x轴有两个交点,
∴b2-4ac>0,∴④正确;
∵抛物线的对称轴x=-$\frac{b}{2a}$=1,
∴-b=2a,
∴2a+b=0,⑤正确.
故选:C.
点评 本题考查的是二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.下列命题中,是真命题的是( )
| A. | 三角形的外角等于它的两个内角 | |
| B. | 面积相等的两个三角形全等 | |
| C. | 三角形的三条高线相交于三角形内一点 | |
| D. | 成轴对称的两个图形是全等图形 |
15.已知关于x的方程$\frac{2x+m}{x+2}$=3的解是负数,则m的取值范围为( )
| A. | m<6 | B. | m<-2 | C. | m>6 | D. | m<6且m≠4 |
12.阅读下面材料:在数学课上,老师提出如下问题:
小涵的主要作法如下:
老师说:“小涵的做法正确的.”
请回答:小涵的作图依据是直径所对的圆周角是直角.
尺规作图,过圆外一点作圆的切线.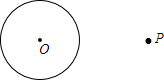 已知:⊙O和点P 求过点P的⊙O的切线 |
| 如图,(1)连结OP,作线段OP的中点A; (2)以A为圆心,OA长为半径作圆,交⊙O于点B,C; (3)作直线PB和PC. 所以PB和PC就是所求的切线.  |
请回答:小涵的作图依据是直径所对的圆周角是直角.
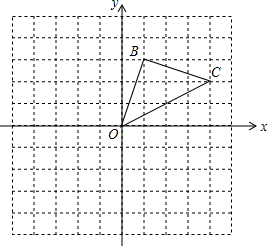 如图,在平面直角坐标系中,三角形OBC的顶点都在网格格点上,一个格是一个单位长度.
如图,在平面直角坐标系中,三角形OBC的顶点都在网格格点上,一个格是一个单位长度.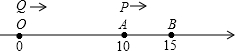 如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.