题目内容
6.设a1,a2,…,a2017是从1,0,-1这三个数中取值的一列数,若a1+a2+…+a2017=84,(a1+1)2+(a2+1)2+…+(a2017+1)2=4001,则a1,a2,…,a2017中为0的个数是201.分析 首先根据(a1+1)2+(a2+1)2+…+(a2017+1)2得到a12+a22+…+a20172+2185,然后设有x个1,y个-1,z个0,得到方程组,$\left\{\begin{array}{l}{x+y+z=2017}\\{1•x+(-1)•y+0•z=84}\\{{1}^{2}x{+(-1)}^{2}y{+0}^{2}z+2185=4001}\end{array}\right.$解方程组即可确定正确的答案.
解答 解:(a1+1)2+(a2+1)2+…+(a2017+1)2=a12+a22+…+a20172+2(a1+a2+…+a2017)+2017
=a12+a22+…+a20172+2×84+2017
=a12+a22+…+a20142+2185,
设有x个1,y个-1,z个0
∴$\left\{\begin{array}{l}{x+y+z=2017}\\{1•x+(-1)•y+0•z=84}\\{{1}^{2}x{+(-1)}^{2}y{+0}^{2}z+2185=4001}\end{array}\right.$,
化简得x-y=84,x+y=1816,
解得x=1450,y=366,z=201,
∴有1450个1,366个-1,201个0,
故答案为:201.
点评 本题考查了数字的变化类问题,解题的关键是对给出的式子进行正确的变形,难度较大.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
15. 如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
 如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )
如图,AB是⊙O的弦,半径OC⊥AB于点D,∠A=36°,点P在圆周上,则∠P等于( )| A. | 27° | B. | 30° | C. | 36° | D. | 40° |
 如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )
如图所示的几何体由一个圆柱体和一个长方体组成,它的主视图是( )



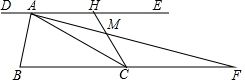 如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.
如图,过锐角△ABC的顶点A作DE∥BC,AB恰好平分∠DAC,AF平分∠EAC交BC的延长线于点F.在AF上取点M,使得AM=$\frac{1}{3}$AF,连接CM并延长交直线DE于点H.若AC=2,△AMH的面积是$\frac{1}{12}$,则$\frac{1}{tan∠ACH}$的值是8-$\sqrt{15}$.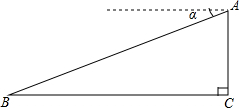 如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)
如图,某飞机于空中A处探测到目标C,此时飞行高度AC=1200m,从飞机上看地平面指挥台B的俯角α=16°31′,则飞机A与指挥台B的距离等于4286m(结果保留整数)(参考数据sin16°31′=0.28,cos16°31′=0.95,tan16°31′=0.30)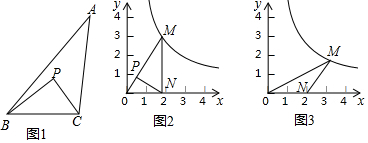
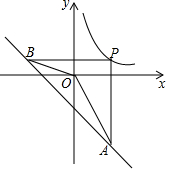 如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )
如图,P为反比例函数y=$\frac{k}{x}$(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=-x-4的图象于点A、B.若∠AOB=135°,则k的值是( )