题目内容
3.如图,两个全等的△ABC和△DFE重叠在一起,固定△ABC,将△DEF进行如下变换:(1)如图1,△DEF沿直线CB向右平移(即点F在线段CB上移动),连接AF、AD、BD.请直接写出S△ABC与S四边形AFBD的关系;
(2)如图2,当点F平移到线段BC的中点时,若四边形AFBD为正方形,那么△ABC应满足什么条件?请给出证明;
(3)在(2)的条件下,将△DEF沿DF折叠,点E落在FA的延长线上的点G处,连接CG,请你在图3的位置画出图形,并求出sin∠CGF的值.

分析 (1)利用平行线的性质以及三角形面积关系得出答案;
(2)利用平行四边形的判定得出四边形AFBD为平行四边形,进而得出AF=$\frac{1}{2}$BC=BF,求出答案;
(3)根据题意画出图形,利用sin∠CGF=$\frac{CF}{CG}$求出即可.
解答 解:(1)S△ABC=S四边形AFBD,
理由:由题意可得:AD∥EC,
则S△ADF=S△ABD,
故S△ACF=S△ADF=S△ABD,
则S△ABC=S四边形AFBD;
(2)△ABC为等腰直角三角形,即:AB=AC,∠BAC=90°,
理由如下:∵F为BC的中点,
∴CF=BF,
∵CF=AD,
∴AD=BF,
又∵AD∥BF,
∴四边形AFBD为平行四边形,
∵AB=AC,F为BC的中点,
∴AF⊥BC,
∴平行四边形AFBD为矩形,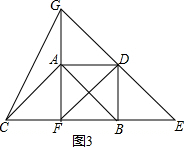
∵∠BAC=90°,F为BC的中点,
∴AF=$\frac{1}{2}$BC=BF,
∴四边形AFBD为正方形;
(3)如图3所示:
由(2)知,△ABC为等腰直角三角形,AF⊥BC,
设CF=k,则GF=EF=CB=2k,
由勾股定理得:CG=$\sqrt{5}$k,
sin∠CGF=$\frac{CF}{CG}$=$\frac{k}{\sqrt{5}k}$=$\frac{\sqrt{5}}{5}$.
点评 此题主要考查了正方形的判定以及等腰直角三角形的性质和锐角三角函数关系等知识,熟练应用正方形的判定方法是解题关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
11.为支持国家南水北调工程建设,小王家由原来养殖户变为种植户,经市场调查得知,种植草莓不超过20亩时,所得利润y(元)与种植面积m(亩)满足关系式y=1500m;超过20亩时,y=1380m+2400.而当种植樱桃的面积不超过15亩时,每亩可获得利润1800元;超过15亩时,每亩获得利润z(元)与种植面积x(亩)之间的函数关系如下表(为所学过的一次函数、反比例函数或二次函数中的一种).
(1)设小王家种植x亩樱桃所获得的利润为P元,直接写出P关于x的函数关系式,并写出自变量的取值范围;(2)如果小王家计划承包40亩荒山种植草莓和樱桃,当种植樱桃面积x(亩)满足0<x<20时,求小王家总共获得的利润w(元)的最大值.
| x(亩) | 20 | 25 | 30 | 35 |
| z(元) | 1700 | 1600 | 1500 | 1400 |
15.下列事件是必然事件的为( )
| A. | 明天太阳从西方升起 | |
| B. | 掷一枚硬币,正面朝上 | |
| C. | 打开电视机,正在播放“河池新闻” | |
| D. | 任意-个三角形,它的内角和等于180° |
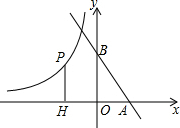 如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
如图,直线y=-$\sqrt{3}$x+3分别与x轴、y轴交于A、B两点,点P是y=-$\frac{\sqrt{3}}{x}$(x<0)的图象上一点,PH⊥x轴于H,当以P为圆心,PH为半径的圆与直线AB相切时,OH的长为$\frac{\sqrt{15}-\sqrt{3}}{2}$.
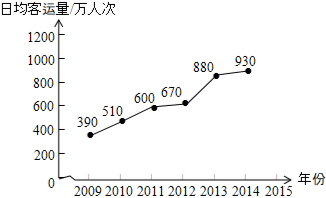 北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..
北京市2009-2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约980万人次,你的预估理由是因为2012-2013年发生数据突变,故参照2013-2014增长进行估算..