题目内容
8．若四边形ABCD为⊙O内接四边形，∠BOD=100°，则∠BAD的度数为50°．分析 根据题意画出图形，再由圆周角定理即可得出结论．
解答 
解：如图所示，
∵∠BOD=100°，
∴∠BAD=$\frac{1}{2}$∠BOD=50°．
故答案为：50°．
点评 本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
16．用因式分解法解一元二次方程x（x-3）=x-3时，原方程可化为（ ）
| A． | （x-1）（x-3）=0 | B． | （x+1）（x-3）=0 | C． | x （x-3）=0 | D． | （x-2）（x-3）=0 |
3．关于中心对称的两个图形，对应线段的关系是（ ）
| A． | 相等 | B． | 平行 | ||
| C． | 相等且平行 | D． | 相等且平行或相等且在同一直线上 |
13．
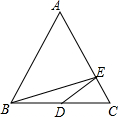如图，已知点D是等边三角形ABC中BC的中点，BC=2，点E是AC边上的动点，则BE+ED的和最小值为（ ）
如图，已知点D是等边三角形ABC中BC的中点，BC=2，点E是AC边上的动点，则BE+ED的和最小值为（ ）| A． | $\sqrt{5}$ | B． | $\sqrt{7}$ | C． | 3 | D． | $\sqrt{3}+1$ |
17．下列运算中错误的是（ ）
| A． | $\sqrt{2}×\sqrt{3}=\sqrt{6}$ | B． | $2\sqrt{2}+3\sqrt{2}=5\sqrt{2}$ | C． | $\frac{1}{{\sqrt{2}}}=\frac{{\sqrt{2}}}{2}$ | D． | $\sqrt{{{（\sqrt{2}-\sqrt{3}）}^2}}=\sqrt{2}-\sqrt{3}$ |
18．
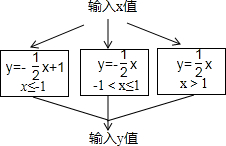根据如图所示的程序计算函数值，若输入的x值为$-\frac{3}{2}$，则输出的结果y应为（ ）
根据如图所示的程序计算函数值，若输入的x值为$-\frac{3}{2}$，则输出的结果y应为（ ）| A． | $\frac{7}{4}$ | B． | $-\frac{3}{4}$ | C． | $\frac{1}{4}$ | D． | $\frac{9}{2}$ |