题目内容
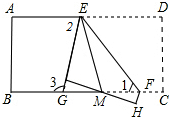 把一张长方形纸片ABCD沿EF折叠,点B、C分别落在G、H的位置上,GH与CD相交于点M,EG的延长线与CD相交于点N,若∠1=55°,求∠2、∠3的度数.
把一张长方形纸片ABCD沿EF折叠,点B、C分别落在G、H的位置上,GH与CD相交于点M,EG的延长线与CD相交于点N,若∠1=55°,求∠2、∠3的度数.考点:平行线的性质,翻折变换(折叠问题)
专题:
分析:由平行的性质可求得∠DEF,结合折叠的性质可求得∠2,再利用平行的性质可求得∠3.
解答:解:
∵ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠1=55°,
又由折叠的性质可知∠GEH=∠DEF=55°,
∴∠2=180°-∠GED=180°-2×55°=70°;
又AD∥BC,
∴∠3+∠2=180°,
∴∠3=180°-∠2=180°-70°=110°.
∵ABCD为长方形,
∴AD∥BC,
∴∠DEF=∠1=55°,
又由折叠的性质可知∠GEH=∠DEF=55°,
∴∠2=180°-∠GED=180°-2×55°=70°;
又AD∥BC,
∴∠3+∠2=180°,
∴∠3=180°-∠2=180°-70°=110°.
点评:本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行?同位角相等,②两直线平行?内错角相等,③两直线平行?同旁内角互补,④a∥b,b∥c?a∥c.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
质量员抽查某零件的质量,超过规定尺寸记为正数,不足规定尺寸记为负数,结果第一个为0.14mm,第二个为-0.13mm,第三个为0.11mm,第四个为-0.10mm,则质量最好的零件是( )
| A、第一个 | B、第二个 |
| C、第三个 | D、第四个 |
已知m满足m2-3m-5=0,则6m-2m2-2014的值为( )
| A、-2004 | B、2004 |
| C、-2024 | D、2024 |
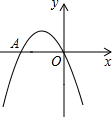 如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).
如图,二次函数y=x2+bx+c的图象经过坐标原点,且与x轴交于A(-2,0).