题目内容
如图1是一种机械装置,直线BC为地面,所在等边△ABC是固定支架,机械臂AD以A为圆心,进行摆动,同时,机械臂DM以D为圆心转动.

已知:A距地面高度是5.9米,AD长4米,DM长1米,
(1)这个机械运动时,请直接写出:AM的最大值是 ;
(2)若AM与⊙D相切,求A、M的距离;
(3)如图2,若机械臂从AD1的位置旋转60°后到AD2的位置,此时∠AD2C=150°,且D2C=3,求BD2的长,并直接写出这个旋转过程中BM的最小值.

已知:A距地面高度是5.9米,AD长4米,DM长1米,
(1)这个机械运动时,请直接写出:AM的最大值是
(2)若AM与⊙D相切,求A、M的距离;
(3)如图2,若机械臂从AD1的位置旋转60°后到AD2的位置,此时∠AD2C=150°,且D2C=3,求BD2的长,并直接写出这个旋转过程中BM的最小值.
考点:圆的综合题,线段的性质:两点之间线段最短,等边三角形的判定与性质,勾股定理,切线的性质,旋转的性质
专题:动点型
分析:(1)根据“两点之间线段最短”可得AM≤AD+DM,从而可以求出AM的最大值.
(2)由AM与⊙D相切可得∠AMD=90°,利用勾股定理就可解决问题.
(3)由于已知线段AD2和CD2与要求的线段BD2有一个公共端点,很难联系起来,可通过旋转(将△CD2B绕着点C顺时针旋转60°到达△CEA的位置),从而将这三条线段转化到同一个三角形中,然后运用勾股定理即可求出BD2;要使得BM最小,只需点M在线段BD上且BD最小,因此点M在图4位置时BM最小,就可求出BM的最小值.
(2)由AM与⊙D相切可得∠AMD=90°,利用勾股定理就可解决问题.
(3)由于已知线段AD2和CD2与要求的线段BD2有一个公共端点,很难联系起来,可通过旋转(将△CD2B绕着点C顺时针旋转60°到达△CEA的位置),从而将这三条线段转化到同一个三角形中,然后运用勾股定理即可求出BD2;要使得BM最小,只需点M在线段BD上且BD最小,因此点M在图4位置时BM最小,就可求出BM的最小值.
解答:解:(1)根据“两点之间线段最短”可得AM≤AD+DM,即AM≤5.
当点M在线段AD2的延长线上时,AM达到最大,最大值为5米.
故答案为:5米.
(2)如图3,
∵AM与⊙D相切,
∴∠AMD=90°.
∵AD=4,DM=1,
∴AM=
=
=
.
∴当AM与⊙D相切时,A、M之间的距离为
.
(3)由于△ABC是等边三角形,
因此将△CD2B绕着点C顺时针旋转60°后到达△CEA的位置,如图4,
则有AE=BD2,CE=CD2,∠ECD2=60°.
∴△CED2是等边三角形.
∴ED2=CD2=3,∠CD2E=60°.
∵∠AD2C=150°,
∴∠AD2E=90°.
∵AD2=4,ED2=3,
∴AE=5.
∴BD2=5.
根据“两点之间线段最短”可得:当点M在线段BD上且BD最小时BM最短,
因此当点M在图4位置时BM最小,最小值为4.
当点M在线段AD2的延长线上时,AM达到最大,最大值为5米.

故答案为:5米.
(2)如图3,
∵AM与⊙D相切,
∴∠AMD=90°.
∵AD=4,DM=1,
∴AM=
| AD2-MD2 |
| 42-12 |
| 15 |
∴当AM与⊙D相切时,A、M之间的距离为
| 15 |
(3)由于△ABC是等边三角形,
因此将△CD2B绕着点C顺时针旋转60°后到达△CEA的位置,如图4,
则有AE=BD2,CE=CD2,∠ECD2=60°.

∴△CED2是等边三角形.
∴ED2=CD2=3,∠CD2E=60°.
∵∠AD2C=150°,
∴∠AD2E=90°.
∵AD2=4,ED2=3,
∴AE=5.
∴BD2=5.
根据“两点之间线段最短”可得:当点M在线段BD上且BD最小时BM最短,
因此当点M在图4位置时BM最小,最小值为4.
点评:本题在图形的运动变化中考查了切线的性质、旋转的性质、等边三角形的判定与性质、勾股定理、两点之间线段最短等知识,有一定的综合性,而通过旋转变换将共顶点的三条线段转化到同一个三角形中是解决第三小题的关键.

练习册系列答案
相关题目
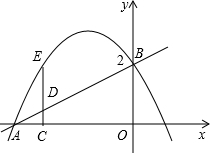 如图,在平面直角坐标系中,直线
如图,在平面直角坐标系中,直线 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是 如图,△ABC中,∠C=90°,CD是AB上的中线,AB=10,则CD=
如图,△ABC中,∠C=90°,CD是AB上的中线,AB=10,则CD=