题目内容
4.(1)计算:$\sqrt{18}$+($\sqrt{2}$+1)0-($\frac{1}{2}$)-1-$\sqrt{2}$tan45°+|-$\sqrt{2}$|.(2)先化简:(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$,然后请你从-2≤x≤2的范围内取一个合适的整数x的值代入求值.
分析 (1)原式利用二次根式性质,零指数幂、负整数指数幂法则,特殊角的三角函数值,以及绝对值的代数意义化简,计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,确定出整数x的值,代入计算即可求出值.
解答 解:(1)原式=3$\sqrt{2}$+1-2-$\sqrt{2}$+$\sqrt{2}$=3$\sqrt{2}$-1;
(2)原式=$\frac{x-2}{x-1}$•$\frac{(x+1)(x-1)}{(x-2)^{2}}$=$\frac{x+1}{x-2}$,
由-2≤x≤2,得到x=-2,-1,0,1,2,
经检验x=-1,1,2时,原式没有意义,
则x=0时,原式=-$\frac{1}{2}$.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
19.若二次根式$\frac{\sqrt{x+1}}{2}$在实数范围内有意义,则x的取值范围是( )
| A. | x≥-1 | B. | x≠2 | C. | x≥-1且x≠2 | D. | 以上都不正确 |
9.已知关于x的方程x2+m2x-2=0的一个根是1,则m的值是( )
| A. | 1 | B. | 2 | C. | ±1 | D. | ±2 |
 已知:∠MAN,求作一个菱形ABCD,使∠MAN为菱形ABCD的一个内角.(尺规作图,不写作法,保留作图痕迹)
已知:∠MAN,求作一个菱形ABCD,使∠MAN为菱形ABCD的一个内角.(尺规作图,不写作法,保留作图痕迹)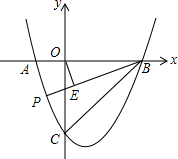 抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标.
抛物线y=x2-2x-3交x轴于A、B两点(A在B的左侧),交y轴于点C,P是第三象限的抛物线上一点,OE⊥PB于E,连接CE,当∠PEC=45°时,求点P的坐标. 如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).
如图所示,A(1,0)、点B在y轴上,将三角形OAB沿x轴负方向平移,平移后的图形为三角形DEC,且点C的坐标为(-3,2).