题目内容
16.若非零实数a,b(a≠b)满足a2+a-2014=0,b2+b-2014=0,求$\frac{1}{a}$+$\frac{1}{b}$的值.分析 利用根与系数的关系求出a+b=-1,ab=-2014,再把$\frac{1}{a}$+$\frac{1}{b}$变成$\frac{a+b}{ab}$,然后把前面的关系式代入即可求出代数式的值.
解答 解:∵实数a、b(a≠b)分别满足a2+a-2014=0,b2+b-2014=0,
∴实数a、b是方程x2+x-2014=0的两根.
由根与系数的关系可知a+b=-1,ab=-2014.
∴$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\frac{1}{2014}$.
点评 本题主要考查一元二次方程根与系数的关系,熟练掌握根与系数关系的公式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6. 如图,A,B,C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )
如图,A,B,C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )
 如图,A,B,C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )
如图,A,B,C是⊙O上的三点,且∠ABC=70°,则∠AOC的度数是( )| A. | 35° | B. | 140° | C. | 70° | D. | 70°或140° |
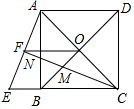 如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.
如图,正方形ABCD的边长为1,对角线AC,BD相交于点O,延长CB至点E,使CE=CA,连接AE,在AB上取一点N,使BN=BE,连接CN并延长,分别交BD,AE与点M,F,连接FO.